CBSE Class 10 Maths Notes Chapter 8 Introduction to Trigonometry are an excellent resource, for knowing all the concepts of a particular chapter in a crisp, and friendly manner. Our articles, help students learn in their language, with proper images, and solved examples for better understanding the concepts.
Chapter 8 of the NCERT Class 10 Maths textbook delves into the world of Introduction to Trigonometry used in real life and covers various topics such as what is trigonometry, fundamentals of trigonometric ratios like sine, cosine, secant, tangent, cosecant, cotangent, and identities. These notes are designed to provide students with a comprehensive summary of the entire chapter and include all the essential topics, formulae, and concepts needed to succeed in their exams.
What is Trigonometry?
Trigonometry was introduced by Aryabhatta, an Indian mathematician, in his book Aryabhattam. Trigonometry shows the relationship of angles with the sides of a triangle. Trigonometry forms the basis of modern science, for example, the behaviour of how light travels is shown by the sine-cosine relationship, Newton’s laws of motion are derived from the roots of trigonometry, measuring heights of buildings, without measuring them, etc.
Adjacent and Opposite side of a Right-Angle Triangle
Before starting our discussion with the Trigonometry ratios, we need to understand what is said to be an adjacent side and an opposite side in a right-angle triangle. A point to note is that trigonometric ratios can only be applied to the right-angled triangles. Let us understand adjacent and opposite sides with the below 2 examples.
Example 1: Given a right-angle triangle ABC, and ∠ACB = θ, our task is to determine what are the adjacent, and opposite sides of a right-angle triangle.
As, we are looking at ∠ACB, our adjacent side is BC, and our opposite side is AB.
Example 2: Given a right-angle triangle ABC, and ∠CAB = θ, our task is to determine what are the adjacent, and opposite sides of a right-angle triangle.
As, we are looking at ∠CAB, our adjacent side is AB, and our opposite side is BC.
Trigonometric Ratios
There are a total of 6 trigonometric ratios, which form the basis of trigonometry i.e. sine, cosine, secant, tangent, cotangent, and cosecant. All, the required ratios, are useful in establishing the relation between angle and lengths.
Given a triangle, ABC, our task is to determine trigonometric ratios for ∠ACB = θ.
Sine Ratio
Sine was the first trigonometric ratio introduced. The sine of an angle is equal to the ratio of the opposite side, and the hypotenuse of a right-angle triangle. In general, it is written as a sin.
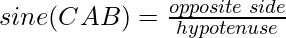
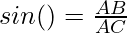
Cosine Ratio
Cosine is complementary to sine. The cosine of an angle is equal to the ratio of the adjacent side, and the hypotenuse of a right-angle triangle. In general, it is written as cos.
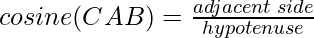
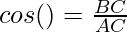
Tangent Ratio
The tangent of an angle is equal to the ratio of the opposite side, and the adjacent side of a right-angle triangle. In general, it is written as tan.
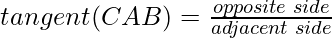
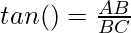
Secant Ratio
Secant is the reverse of the sine. The secant of an angle is equal to the ratio of the hypotenuse and the adjacent side of a right-angle triangle. In general, it is written as sec.
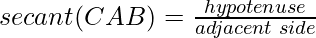
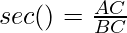
Cosecant Ratio
Cosecant is the reverse of the cosine. the cosecant of an angle is equal to the ratio of the hypotenuse and the adjacent side of a right-angle triangle. In general, it is written as cosec.

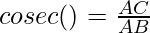
Cotangent Ratio
The cotangent of an angle is equal to the ratio of the adjacent side, and the opposite side of a right-angle triangle. In general, it is written as a cot.
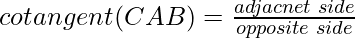
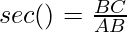
Example: Given sin θ = 4/5. Find all trigonometric ratios for angle θ.
Solution:
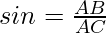
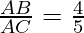
Hence, AB = 4, AC = 5
Apply pythogoras theorem,
AB2 + BC2 = AC2
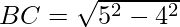
BC = 3
Hence, all trigonometric ratios are,
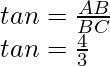
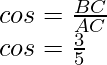
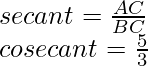
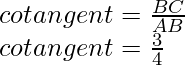
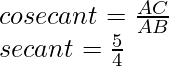
Trigonometric Tables
Measuring values of sin, cos, tan, cot, sec, and cosec, in precise terms is quite a difficult task without a calculator. But this is not true, for all angles, there are 5 special angles, whose value can precisely be written, and also helps in dealing with most of the maths problems. These angles are 0°, 30°, 45°, 60° and 90°.
The below table provides the list of all trigonometric ratios, with the values of the special angles. The proof of them does not hold significance from the exam point of view.
∠A
| 0°
| 30°
| 45°
| 60°
| 90°
|
|---|
sin A
| 0
| 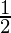
| 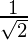
| 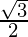
| 1
|
|---|
cos A
| 1
| 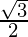
| 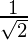
| 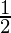
| 0
|
|---|
tan A
| 0
| 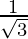
| 1
| 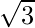
| Not Defined
|
|---|
sec A
| 1
| 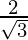
| 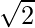
| 2
| Not Defined
|
|---|
cosec A
| Not Defined
| 2
| 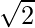
| 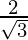
| 1
|
|---|
cot A
| Not Defined
| 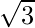
| 1
| 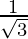
| 0
|
|---|
Example: In triangle ABC, right-angle at B. BC = 3, and AC = 6. Find angles ∠BCA, and ∠CAB.
Solution:
Let us say, ∠BCA = θ, and ∠CAB = α,
We know that,
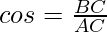
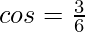
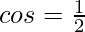
From the above table, we know that,
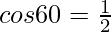
Hence, ∠BCA = θ = 60°
By, triangle property, sum of three sides of a triangle is 180°.
θ + α + 90° = 180°
α = 180° – 90° – 60°
Hence, α = ∠CAB = 30°
Range of Trigonometric Functions
The first quadrant signifies the range of angle can be from 0° to 90°. The values given by the trigonometric function, between these angles are called the range of the trigonometric function. For example, the value of sin0°, is 0, sin45°, is 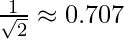 , and the value of sin 90° is 1. It shows that the range of sin is [0, 1], and the value of sin, increases in between this range. The below table shows the list of the range of trigonometric functions and their monotonic nature.
, and the value of sin 90° is 1. It shows that the range of sin is [0, 1], and the value of sin, increases in between this range. The below table shows the list of the range of trigonometric functions and their monotonic nature.
Note: Monotonic means that, either the function will only increase or only decrease.
∠A
| Range
| Monotonicity
|
sin A
| [0, 1]
| Increasing
|
cos A
| [1, 0]
| Decreasing
|
tan A
| [0, ∞]
| Increasing
|
sec A
| [1, ∞]
| Increasing
|
cosec A
| [∞, 1]
| Decreasing
|
cot A
| [∞, 0]
| Decreasing
|
Trigonometric Identities
Identities are the equations, which are true for any value of a variable. We have 3 different types of trigonometric identities i.e. Pythagorean identity, reciprocal identity, and quotient identity.
Pythagorean Identity
At this level, we only have 3 Pythagorean identities in our syllabus. The proof of them is not significant to us. Below is the list showing the trigonometric identities.
- cos2A + sin2A = 1
- 1 + tan2A = sec2A
- 1 + cot2A = cosec2A
Reciprocal Identity
If observed carefully, then, we can find that many trigonometric ratios are just the reverse of each other. We have 3 reciprocal identities listed below:
- sec θ = 1/cos θ
- cosec θ = 1/sin θ
- cot θ = 1/tan θ
Quotient Identity
tan θ and cot θ can be rewritten in terms of sinθ and cosθ.
- tanθ = sinθ/cosθ,
- cotθ = cosθ/sinθ
Example: Prove that, 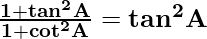
Solution:
From Trigonometric Identity,
1 + tan2A = sec2A, and
1 + cot2A = cosec2A
Hence, the equation can be rewritten as,
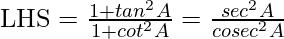
Also, secA = 1/cosA, cosecA = 1/sinA,
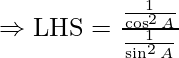
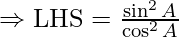
⇒ LHS = tan2A
Hence, L.H.S. = R.H.S.
Also, Read
FAQs on NCERT Notes for Class 10 Maths Chapter 8 Introduction to Trigonometry
Q1: What is Trigonometry?
Answer:
It is the branch of maths which deals with the angles, and it’s relationship with the sides of a triangle.
Q2: How many Trigonometric functions are there?
Answer:
There are 7 Trigonometric functions i.e. sin, cos, tan, sec, cosec, and cot.
Q3: Is Secant, a monotonically increasing or decreasing function in between 0° and 90°?
Answer:
Secant is a monotonically increasing function, because secA = 1/cosA, and cosA, is a monotonically decreasing function.
Q4: Are Equation and Identity the same?
Answer:
No, every identity is an equation, but every equation is not an identity. Identity, is term used for the equations, in which all variables values, give a possible solution. For example, Pythagoras theorem AB2 + BC2 = AC2, this equation is true for any value of AB, BC, and AC, if they form a trangle, hence, it’s an identity, but let us consider the equation 2x + 4 = 6, this equation is only true, when x = 1, hence, it’s an equation.
Q5: What are Pythagorean Identities?
Answer:
As the name suggests, these identities are obtained from the pythogoras theorem. Some pythagorean identities are shown below:
- sin2A + cos2A = 1
- 1 + tan2A = sec2A
- 1 + cot2A = cosec2A
Share your thoughts in the comments
Please Login to comment...