Introduction to Grover’s Algorithm

• Grover’s algorithm is a quantum algorithm that solves the unstructured search problem. In an unstructured search problem, we are given a set of N elements and we want to find a single marked element. A classical computer would need to search through all N elements in order to find the marked element, which would take time O(N). Grover’s algorithm, on the other hand, can find the marked element in time  O(√ N).
• Grover’s algorithm is a powerful tool that can be used to solve a variety of problems. For example, it can be used to find patterns in data, break cryptographic keys, and solve optimization problems. As quantum computers become more powerful, Grover’s algorithm will become increasingly important.

Algorithm:

The algorithm works by applying a series of quantum operations to the input state, which is initialized as a superposition of all possible search states. The key idea behind Grover’s algorithm is to amplify the amplitude of the marked state (i.e., the state containing the item that we are searching for) by iteratively applying a quantum operation known as the Grover operator.

The Grover operator has two quantum operations: 

• The reflection on the mean 
• The inversion of the marked state. 

Here is a more detailed explanation of how Grover’s algorithm works:

1. Initial state:

The algorithm starts in a state that is a superposition of all N elements. This state can be written as:

where ∣x⟩ is the state corresponding to the element x.

2. Diffusion operator:

The diffusion operator is a quantum operation that amplifies the amplitudes of the states that correspond to the marked element. The diffusion operator can be written as

where I is the identity operator.

3. Measurement:

The algorithm measures the state of the system. This collapses the superposition and gives us the marked element. The repeated use of this operator increases the scope of the specified condition, making it easier to measure. Once the specified state is reached, the algorithm returns the index of the object corresponding to that state.

Proof of correctness:

The proof of the correctness of Grover’s algorithm can be shown through the following steps:

• Initialization: The algorithm begins with an input state, which is initialised as a superposition of all possible search states. The superposition state is given by:            
  |s⟩ = (1/√N)∑x|x⟩        , where |x⟩ represents the state of a particular item in the database, and N is the total number of items.
• Marking the state: The algorithm then applies an oracle function, which marks the state containing the item that we are searching for. The oracle function flips the sign of the amplitude of the marked state: 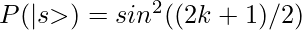, where f(x) = 1 if x is the marked state, and f(x) = 0 otherwise.
• Applying the Grover operator: The Grover operator is then applied iteratively to the state |s’⟩. The Grover operator consists of two quantum operations: the reflection about the mean and the inversion about the marked state. The operator is applied O(sqrt(N)) times to amplify the amplitude of the marked state and decrease the amplitudes of the other states.
• Measuring the state: Finally, the state is measured, and the algorithm returns the index of the marked state.
  • The correctness of the algorithm can be shown by analyzing the probability of measuring the marked state at the end of the algorithm. The probability of measuring the marked state after k iterations of the Grover operator is given by: 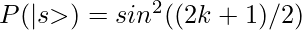, where θ = arcsin(1/√N) is the angle between the initial state and the marked state. As k increases, the probability of measuring the marked state approaches 1.
  • Therefore, Grover’s algorithm can be shown to correctly find the marked state in O(sqrt(N)) time complexity with high probability.

Pseudo Code:

Input: N: number of items in the list, oracle(x): a function that returns true if x is the target item, and false otherwise

Step 1: Initialize state

• Hadamard transform on all qubits

Step 2: Iterate over Grover’s algorithm

for k = 1 to sqrt(N) do

# Step 2a: Apply the oracle

• Apply the oracle to the state

    # Step 2b: Apply the diffusion operator

• Hadamard transform on all qubits
• Apply an X gate on all qubits
• Apply a multi-controlled Z gate (which flips the sign of the state only if all qubits are in the state |1>)
• Apply an X gate on all qubits
• Hadamard transform on all qubits

end for

Step 3: Measure the state and output the result

• Measure the state and output the result

Below is the Implementation of the above Code:

This code describes the Oracle function and the Grover diffusion operator and then uses it to implement the Grover algorithm for a given specified situation. The algorithm uses the Qiskit framework to define and run a quantum circuit in a simulator and returns the results of the measurements as a solution x.

Python3

from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, Aer, execute

# Define the black box function


def oracle(circuit, register, marked_state):
    for i in range(len(marked_state)):
        if marked_state[i] == '1':
            circuit.x(register[i])
    circuit.cz(register[0], register[1])
    for i in range(len(marked_state)):
        if marked_state[i] == '1':
            circuit.x(register[i])

# Define the Grover diffusion operator


def grover_diffusion(circuit, register):
    circuit.h(register)
    circuit.x(register)
    circuit.h(register[1])
    circuit.cx(register[0], register[1])
    circuit.h(register[1])
    circuit.x(register)
    circuit.h(register)

# Define the Grover algorithm


def grover(marked_state):

    # Initialize a quantum register
    # of n qubits
    n = len(marked_state)
    qr = QuantumRegister(n)
    cr = ClassicalRegister(n)
    circuit = QuantumCircuit(qr, cr)

    # Apply the Hadamard gate
    # to each qubit
    circuit.h(qr)

    # Repeat the following procedure
    # O(sqrt(2 ^ n)) times
    num_iterations = int(round((2 ** n) ** 0.5))
    for i in range(num_iterations):
        # Apply the black box function f
        # to the current state to mark
        # the solution
        oracle(circuit, qr, marked_state)

        # Apply the Grover diffusion
        # operator to amplify the amplitude
        # of the marked solution
        grover_diffusion(circuit, qr)

    # Measure the state to obtain
    # a solution x
    circuit.measure(qr, cr)

    # Run the circuit on a simulator
    backend = Aer.get_backend('qasm_simulator')
    job = execute(circuit, backend, shots = 1)
    result = job.result()
    counts = result.get_counts()
    x = list(counts.keys())[0]

    return x


# Test the Grover algorithm
marked_state = '101'
result = grover(marked_state)
print(f"The marked state is {result}")

Output:

Applications of Grover’s Algorithm:

• Data mining: Grover’s algorithm can be used to find patterns in large datasets that would be impossible to find with a classical computer. For example, it could be used to find fraudulent transactions in a financial database or to identify cancer cells in a medical image.
• Cryptography: Grover’s algorithm can be used to break cryptographic keys that are currently considered secure. This could have a major impact on the security of online communications and transactions.
• Optimization: Grover’s algorithm can be used to solve optimization problems that are difficult or impossible to solve with a classical computer. For example, it could be used to find the shortest route between two points or to find the optimal investment portfolio..

Limitations of Grover’s Algorithm:

• Quadratic speedup: Grover’s algorithm gives a quadratic speedup compared to classical algorithms, which means that it can only provide a significant speedup for some problems that have a large search space. For problems with smaller search spaces, the speedup may not be good enough to justify the use of this algorithm.
• Limited by hardware: Grover’s algorithm requires the use of a large number of qubits to achieve a significant speedup, which is currently beyond the capabilities of most quantum hardware. This means that the algorithm may not be practical for many real-world applications until more powerful quantum hardware is developed.
• Limited to unstructured search: Grover’s algorithm is designed for unstructured search problems, which means that it may not be applicable to other types of problems such as optimization or simulation.
• Error-prone: Grover’s algorithm, like all quantum algorithms, is susceptible to errors due to noise and decoherence. These errors can affect the accuracy and reliability of the algorithm, which can limit its practical use in real-world applications.
• Limited applicability in cryptography: Although Grover’s algorithm can be used to break certain cryptographic algorithms, it is not applicable to all types of encryption. For example, public-key encryption is not vulnerable to Grover’s algorithm due to its use of mathematical problems that are not efficiently solvable by quantum computers.

Conclusion:

Overall, Grover’s algorithm is a powerful tool that can be used to solve a variety of problems. For example, it can be used to find patterns in data, break cryptographic keys, and solve optimization problems. As quantum computers become more powerful, Grover’s algorithm will become increasingly important.