Integration in a Polynomial for a given value
Last Updated :
04 Jun, 2021
Given string str which represents a polynomial and a number N, the task is to integrate this polynomial with respect to X at the given value N.
Examples:
Input: str = “90x4 + 24x3 + 18x2 + 18x”, N = 1.
Output: 39
Explanation:
Given, dy/dx = 90*(X4) + 24* (X3) + 18* (X2) + 18*(X). On integrating this equation, we get 18*(X5) + 6*(X4) + 6*(X3) + 9*(X2) and substituting the value X = 1, we get:
18 + 6 + 6 + 9 = 39.
Input: str = “4x3 + 2x2 + 3x”, N = 2
Output: 27
Approach: The idea is to use the identity of the integration. For some given function X with the power of N, the integration of this term is given by:
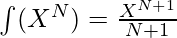
Therefore, the following steps are followed to compute the answer:
- Get the string.
- Split the string and perform the integration based on the above formula.
- Substitute the value of N in the obtained expression.
- Add all the individual values to get the final integral value.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
double inteTerm(string pTerm, ll val)
{
string coeffStr = "";
int i;
for (i = 0; pTerm[i] != 'x'; i++)
coeffStr.push_back(pTerm[i]);
ll coeff = atol(coeffStr.c_str());
string powStr = "";
for (i = i + 2; i != pTerm.size(); i++)
powStr.push_back(pTerm[i]);
ll power = atol(powStr.c_str());
return (coeff * pow(val, power + 1))
/ (power + 1);
}
double integrationVal(string poly, int val)
{
ll ans = 0;
istringstream is(poly);
string pTerm;
while (is >> pTerm) {
if (pTerm == "+")
continue;
else
ans = (ans + inteTerm(pTerm, val));
}
return ans;
}
int main()
{
string str = "4x^3 + 3x^1 + 2x^2";
int val = 2;
cout << integrationVal(str, val);
return 0;
}
|
Java
public class GFG
{
static int inteTerm(String pTerm, int val)
{
String coeffStr = "";
int i = 0;
while (i < pTerm.length() && pTerm.charAt(i) != 'x')
{
coeffStr += pTerm.charAt(i);
i += 1;
}
int coeff = Integer.parseInt(coeffStr);
String powStr = "";
int j = i + 2;
while(j< pTerm.length())
{
powStr += (pTerm.charAt(j));
j += 1;
}
int power = Integer.parseInt(powStr);
return ((coeff * (int)Math.pow(val, power + 1)) / (power + 1));
}
static int integrationVal(String poly, int val)
{
int ans = 0;
String[] stSplit = poly.split(" \\+ ");
int i = 0;
while(i < stSplit.length)
{
ans = (ans + inteTerm(stSplit[i], val));
i += 1;
}
return ans;
}
public static void main(String[] args) {
String st = "4x^3 + 3x^1 + 2x^2";
int val = 2;
System.out.println(integrationVal(st, val));
}
}
|
Python3
def inteTerm(pTerm, val):
coeffStr = ""
i = 0
while (i < len(pTerm) and
pTerm[i] != 'x'):
coeffStr += pTerm[i]
i += 1
coeff = int(coeffStr)
powStr = ""
j = i + 2
while j< len(pTerm):
powStr += (pTerm[j])
j += 1
power = int(powStr)
return ((coeff *
pow(val,
power + 1)) //
(power + 1))
def integrationVal(poly, val):
ans = 0
stSplit = poly.split("+")
i = 0
while i < len(stSplit):
ans = (ans +
inteTerm(stSplit[i],
val))
i += 1
return ans
if __name__ == "__main__":
st = "4x^3 + 3x^1 + 2x^2"
val = 2
print(integrationVal(st, val))
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int inteTerm(string pTerm, int val)
{
string coeffStr = "";
int i = 0;
while (i < pTerm.Length && pTerm[i] != 'x')
{
coeffStr += pTerm[i];
i += 1;
}
int coeff = Convert.ToInt32(coeffStr);
string powStr = "";
int j = i + 2;
while(j< pTerm.Length)
{
powStr += (pTerm[j]);
j += 1;
}
int power = Convert.ToInt32(powStr);
return ((coeff * (int)Math.Pow(val, power + 1)) / (power + 1));
}
static int integrationVal(string poly, int val)
{
int ans = 0;
string[] stSplit = poly.Split('+');
int i = 0;
while(i < stSplit.Length)
{
ans = (ans + inteTerm(stSplit[i], val));
i += 1;
}
return ans;
}
static void Main() {
string st = "4x^3 + 3x^1 + 2x^2";
int val = 2;
Console.WriteLine(integrationVal(st, val));
}
}
|
Javascript
<script>
function inteTerm(pTerm,val)
{
let coeffStr = "";
let i = 0;
while (i < pTerm.length && pTerm[i] != 'x')
{
coeffStr += pTerm[i];
i += 1;
}
let coeff = parseInt(coeffStr);
let powStr = "";
let j = i + 2;
while(j< pTerm.length)
{
powStr += (pTerm[j]);
j += 1;
}
let power = parseInt(powStr);
return Math.floor((coeff * Math.floor(Math.pow(val, power + 1))) / (power + 1));
}
function integrationVal(poly,val)
{
let ans = 0;
let stSplit = poly.split(" + ");
let i = 0;
while(i < stSplit.length)
{
ans = (ans + inteTerm(stSplit[i], val));
i += 1;
}
return ans;
}
let st = "4x^3 + 3x^1 + 2x^2";
let val = 2;
document.write(integrationVal(st, val));
</script>
|
Share your thoughts in the comments
Please Login to comment...