Implementing Shamir’s Secret Sharing Scheme in Python

Secret Sharing schemes are used in the distribution of a secret value among multiple participants (shareholders) by dividing the secret into fragments (shares). This is done in a manner that prevents a single shareholder from having any useful knowledge of the original secret at all. The only way to retrieve the original secret is to combine the shares, distributed among the participants. Hence, the control of the secret is distributed. These schemes are examples of Threshold Cryptosystems, which involve the division of secrets among multiple parties such that several parties (more than some threshold number) must cooperate to reconstruct the secret. 

Fig 1: Depiction of Secret Sharing between n participants

In general, a secret may be split into n shares (for n shareholders), out of which, a minimum of t, (t < n) shares are required for successful reconstruction. Such a scheme is referred to as a (t, n) sharing-scheme. From the n participants, any subset of shareholders, of size greater or equal to t, can regenerate the secret. Importantly, even with any k (k < t) shares, no new information about the original secret is learned. 

Shamir Secret Sharing

Shamir Secret Sharing (SSS) is one of the most popular implementations of a secret sharing scheme created by Adi Shamir, a famous Israeli cryptographer, who also contributed to the invention of RSA algorithm. SSS allows the secret to be divided into an arbitrary number of shares and allows an arbitrary threshold (as long as it is less than the total participants). SSS is based on the mathematical concept of polynomial interpolation which states that a polynomial of degree t-1 can be reconstructed from the knowledge of t or more points, known to be lying on the curve.
For instance, to reconstruct a curve of degree 1 (a straight line), we require at least 2 points that lie on the line. Conversely, it is mathematically infeasible to reconstruct a curve if the number of unique points available is less than (degree-of-curve + 1). One can imagine having infinite possible straight lines that could be formed as a result of just one point in 2D space. 

Motivation behind SSS

The concept of polynomial interpolation can be applied to produce a secret sharing scheme by embedding the secret into the polynomial. A general polynomial of degree p can be expressed as follows:

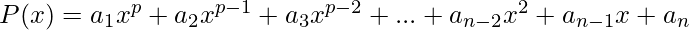
In the expression of P(x), the values a_{1}, a_{2}, a_{3}, …, a_{n} represent the coefficients of the polynomial. Thus, construction of a polynomial requires the selection of these coefficients. Note that no values are actually substituted in for x; every term in the polynomial acts as a “placeholder” to store the coefficient values.  
Once the polynomial is generated, we can essentially represent the curve by just p+1 points that lie on the curve. This follows from the polynomial interpolation principle. For example, a curve of degree 4 can be reconstructed if we have access to at least 5 unique points lying on it. To do this, we can run Lagrange’s interpolation or any other similar interpolation mechanism. 

Fig 2: Example of using Polynomial Interpolation to reconstruct a curve

Consequently, if we conceal the secret value into such a polynomial and use various points on the curve as shares, we arrive at a secret sharing scheme. More precisely, to establish a (t, n) secret sharing scheme, we can construct a polynomial of degree t-1 and pick n points on the curve as shares such that the polynomial will only be regenerated if t or more shares are pooled. The secret value (s) is concealed in the constant term of the polynomial (coefficient of 0-degree term or the curve’s y-intercept) which can only be obtained after the successful reconstruction of the curve.

Algorithm used

Shamir’s Secret Sharing uses the polynomial interpolation principle to perform threshold sharing in the following two phases: 
Phase I: Generation of Shares
This phase involves the setup of the system as well as the generation of the shares. 

1. Decide the values for the number of participants (n) and the threshold (t) to secure some secret value (s)
2. Construct a random polynomial, P(x), with degree t-1 by choosing random coefficients of the polynomial. Set the constant term in the polynomial (coefficient of zero degree term) to be equal to the secret value s
3. To generate the n shares, randomly pick n points lying on the polynomial P(x)
4. Distribute the picked coordinates in the previous step among the participants. These act as the shares in the system

Phase II: Reconstruction of Secret
For reconstruction of the secret, a minimum of t participants are required to pool their shares. 

1. Collect t or more shares
2. Use an interpolation algorithm to reconstruct the polynomial, P'(x), from the shares. Lagrange’s Interpolation is an example of such an algorithm
3. Determine the value of the reconstructed polynomial for x = 0, i.e. calculate P'(0). This value reveals the constant term of the polynomial which happens to be the original secret. Thus, the secret is reconstructed

Below is the implementation. 

Python3

import random
from math import ceil
from decimal import Decimal

FIELD_SIZE = 10**5


def reconstruct_secret(shares):
    """
    Combines individual shares (points on graph)
    using Lagranges interpolation.

    `shares` is a list of points (x, y) belonging to a
    polynomial with a constant of our key.
    """
    sums = 0
    prod_arr = []

    for j, share_j in enumerate(shares):
        xj, yj = share_j
        prod = Decimal(1)

        for i, share_i in enumerate(shares):
            xi, _ = share_i
            if i != j:
                prod *= Decimal(Decimal(xi)/(xi-xj))

        prod *= yj
        sums += Decimal(prod)

    return int(round(Decimal(sums), 0))


def polynom(x, coefficients):
    """
    This generates a single point on the graph of given polynomial
    in `x`. The polynomial is given by the list of `coefficients`.
    """
    point = 0
    # Loop through reversed list, so that indices from enumerate match the
    # actual coefficient indices
    for coefficient_index, coefficient_value in enumerate(coefficients[::-1]):
        point += x ** coefficient_index * coefficient_value
    return point


def coeff(t, secret):
    """
    Randomly generate a list of coefficients for a polynomial with
    degree of `t` - 1, whose constant is `secret`.

    For example with a 3rd degree coefficient like this:
        3x^3 + 4x^2 + 18x + 554

        554 is the secret, and the polynomial degree + 1 is
        how many points are needed to recover this secret.
        (in this case it's 4 points).
    """
    coeff = [random.randrange(0, FIELD_SIZE) for _ in range(t - 1)]
    coeff.append(secret)
    return coeff


def generate_shares(n, m, secret):
    """
    Split given `secret` into `n` shares with minimum threshold
    of `m` shares to recover this `secret`, using SSS algorithm.
    """
    coefficients = coeff(m, secret)
    shares = []

    for i in range(1, n+1):
        x = random.randrange(1, FIELD_SIZE)
        shares.append((x, polynom(x, coefficients)))

    return shares


# Driver code
if __name__ == '__main__':

    # (3,5) sharing scheme
    t, n = 3, 5
    secret = 1234
    print(f'Original Secret: {secret}')

    # Phase I: Generation of shares
    shares = generate_shares(n, t, secret)
    print(f'Shares: {", ".join(str(share) for share in shares)}')

    # Phase II: Secret Reconstruction
    # Picking t shares randomly for
    # reconstruction
    pool = random.sample(shares, t)
    print(f'Combining shares: {", ".join(str(share) for share in pool)}')
    print(f'Reconstructed secret: {reconstruct_secret(pool)}')

Output:

Original Secret: 1234
Shares: (79761, 4753361900938), (67842, 3439017561016), (42323, 1338629004828), (68237, 3479175081966), (32818, 804981007208)
Combining shares: (32818, 804981007208), (79761, 4753361900938), (68237, 3479175081966)
Reconstructed secret: 1234

Practical Applications

Secret sharing schemes are widely used in cryptosystems where trust is required to be distributed instead of centralized. Prominent examples of real world scenarios where secret sharing is used include: 

• Threshold Based Signatures for Bitcoin
• Secure Multi-Party Computation
• Private Machine Learning with Multi Party Computation
• Management of Passwords