The equality of matrices is a mathematical concept where two or more matrices are equal when compared. Before learning the concept of equality of matrices, we need to know what a matrix is. A rectangle or square-shaped array of numbers or symbols organized in rows and columns to represent a mathematical object or one of its attributes is called a matrix in mathematics. The horizontal lines are said to be rows, while the vertical lines are said to be columns. For example, 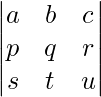 is a matrix with 3 rows and 3 columns. It can be called a “3 by 3” matrix and is a square matrix. On the other hand,
is a matrix with 3 rows and 3 columns. It can be called a “3 by 3” matrix and is a square matrix. On the other hand, 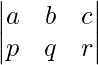 is a “2 by 3” matrix and is a rectangular matrix.
is a “2 by 3” matrix and is a rectangular matrix.
What is Equality of Matrices?
When two or more matrices are equal, it is referred to as the equality of matrices. Matrices are considered to be equal if they have the same number of rows and columns, as well as the same number of elements. Equality of matrices does not hold for either of the previously mentioned conditions. The two matrices are said to be unequal if the order of the matrices is not equal or at least one pair of the corresponding elements is not equal. This concept is relevant for both- rectangular and square matrices.
Conditions for Equality Matrices
The equality of matrices is a concept of matrices that are defined by comparing two or more matrices that have the same dimensions and all the same corresponding elements. If “A = [aij]m×n” and “B = [bij]p×q” are two matrices, then the following are three requirements for matrix equality for matrices:
- The number of rows in matrices A and B is the same, i.e., m = p.
- The number of columns in matrices A and B is the same, i.e., n = q.
- For any i and j, the corresponding elements of A and B are equal, i.e., aij = bij.
Example:
Say 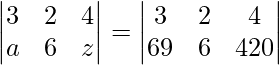 . Find the values of a and z.
. Find the values of a and z.
Because the order of the two matrices is equal, matrices are equal if and only if their corresponding elements are likewise equal.
Thus, comparing a and c to the corresponding elements of the other matrix, we have a = 69 and z = 420.
Solving Equality of Matrices
We have learned what is meant by the equality of matrices and also the conditions that are required for the equality of matrices. Now, let us solve the equality of matrices. For example, let us consider two matrices, A = [aij] and B = [bij]. Now, the two matrices A and B are said to be equal if and only if the order of both matrices is the same and also their corresponding elements are equal, i.e., aij = bij for all i and j.
First, let us consider two equal matrices A and B.
![Rendered by QuickLaTeX.com A = \left[\begin{array}{cc} 7 & 2a+3b\\ 1 & 8 \end{array}\right] and B = \left[\begin{array}{cc} 7 & 5\\ a+b & 8 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3eed58faa7c060cd5b9a3a25c5c6294a_l3.png)
As the given matrices are equal, so A = B.
![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 7 & 2a+3b\\ 1 & 8 \end{array}\right] = \left[\begin{array}{cc} 7 & 5\\ a+b & 8 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54f176e95fe4acd5a119730348976542_l3.png)
We can see that the order of the given matrices is equal, so the equality of matrices holds if and only if the corresponding elements are also equal.
So, 2a + 3b = 5 ⇢ (1)
a + b = 1 ⇢ (2)
a = 1 − b ⇢ (3)
Now, substitute the value of a = 1 − b in equation (1)
⇒ 2 (1 − b) + 3b = 5
⇒ 2 − 2b + 3b = 5
⇒ 2 + b = 5
⇒ b = 5 − 2 = 3
Now, substitute the value of b =3 in equation (3)
⇒ a = 1 − 3 = −2
Thus, the given matrices are said to be equal if a = −2 and b =3.
Sample Problems
Problem 1: Are the matrices ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 2 & 3 & 6 \\ 4 & 5 & 7 \\ 1 & -3 & -12 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a3b4350b39e830cb1d9aa3bee6a56211_l3.png) and
and ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} -1 & 3 & 6 \\ 4 & 5 & 7 \\ 1 & -3 & -12 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d06386e61b57f09a66952d7d07eb848d_l3.png) equal?
equal?
Solution:
The given matrices have the same order, which means they have the same number of rows and columns. As a result, the first criterion for matrix equality has been met. The first condition of equality of matrices is fulfilled. Now the second condition, i.e., the corresponding elements must be equal needs to be examined. As can be seen, the element in the first row and first column of the first matrix is 2 in the first matrix and -1 in the second matrix, indicating that not all the elements are equal.
Hence the two matrices are not equal.
Problem 2: Find the values of a, b, x if A = [a+b 6 8 2x 3b] and B = [3 6 8 14 9] are equal.
Solution:
Since A and B are given to be equal matrices, therefore their corresponding elements are also equal. We have
a + b = 3, 2x = 14, 3b = 9
⇒ x = 24/2 = 12, b = 9/3 = 3
⇒ a + 3 = 3 [From b = 3]
⇒ a = 0
⇒ a = 0, b = 3, x = 7
Problem 3: If ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 3x+4y & x-2y & 6 \\ a+b & -3 & 2a-b \end{array}\right] = \left[\begin{array}{ccc} 2 & 4 & 6 \\ 5 & -3 & -5 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a7141fbd5b3eaaacc28157f82148cd73_l3.png) , find the values of a, b, x and y.
, find the values of a, b, x and y.
Solution:
3x + 4y = 2, ⇢ (1)
x – 2y = 4, ⇢ (2)
a + b = 5, ⇢ (3)
2a – b = -5 ⇢ (4)
Solving equations (1) and (2),
x = 2y + 4 [From (2)]
Substituting the above in (1),
3(2y + 4) + 4y = 2
⇒ 6y + 12 + 4y = 2
⇒ 10y = 2 – 12
⇒ 10y = -10
⇒ y = -1
⇒ x = 2(-1) + 4
= -2 + 4
= 2
Similarly, solving equations (3) and (4), we have a = 0 and b = 5.
Problem 4: From the definition of the equality of matrices, determine whether the matrices given below are equal or not.
![Rendered by QuickLaTeX.com M = \left[\begin{array}{cc} 21 & 15\\ 3 & 5\\ 8 & 16 \end{array}\right] and N = \left[\begin{array}{cc} 21 & 15\\ 3 & 7\\ 8 & 16 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a972c6efe7c88177aded93e652dc7ff_l3.png)
Solution:
The order of the given matrices M and N is “3 × 2,” i.e., they have 3 rows and 2 columns. So, both matrices have the same number of rows and columns. So, the first two conditions for the equality of matrices are satisfied.
Now, let us check the corresponding elements of the given two matrices. We can see that the element in the second row and second column of the matrix M is 5, whereas the matrix N is 7. As 3 ≠ 7, the given matrices do not follow the third condition, i.e., the corresponding elements of the given matrices must be the same.
Therefore, the given matrices M and N are not equal.
Problem 5: If A and B are equal matrices, and A = [6 -12 18 24], then what is matrix B?
Solution:
Given that, A and B are equal matrices.
The order of matrix A is “1 × 4.”
So, the order of the matrix B must be the same, i.e., “1 × 4.”
We know that the equality of matrices holds for those that have the same dimensions and all the same corresponding elements.
Now, the required matrix B = [6 -12 18 24].
Problem 6: If ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}3& x+y\\x-y&5\end{array}\right]=\left[\begin{array}{ccc}3&-7\\2&5\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e5551352ce2ef4d85212339165a68465_l3.png) , find the values of x and y.
, find the values of x and y.
Since A and B are given to be equal matrices, therefore their corresponding elements are also equal. We have
x + y = -7
x – y = 2
Adding the two equations, we have:
2x = -5
x = -5/2
So -5/2 -2 = 7
y = 9/2
Problem 7: Are the matrices ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 1 & 2 & 3 \\ 8 & 4 & 6 \\ 4 & 5 & 7 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4eb1a57830d7f997fa85252ce620a9ae_l3.png) and
and ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 1 & 2 & 3 \\ 8 & 5 & 6 \\ 4 & 5 & 7 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f7cf187fe2fe4ccdc889bc39e0498f5e_l3.png) equal?
equal?
Solution:
The given matrices have the same order, which means they have the same number of rows and columns. As a result, the first criterion for matrix equality has been met. The first condition of equality of matrices is fulfilled. Now the second condition, i.e., the corresponding elements must be equal needs to be examined. As can be seen, the element in the second row and second column of the first matrix is 4 in the first matrix and 5 in the second matrix, indicating that not all the elements are equal.
Hence the two matrices are not equal.
FAQs on Equality of Matrices
Question 1: What is the Equality of Matrices?
Answer:
The equality of matrices is a concept of matrices that is defined by comparing two or more matrices that have the same dimensions and all the same corresponding elements.
Question 2: What are the conditions for the Equality of Matrices?
Answer:
The following are necessary conditions that are required for the equality for matrices A = [aij]m×n and B = [bij]p×q to be true:
Matrices A and B must have the same number of rows, i.e., m = p.
Matrices A and B must have the same number of columns, i.e., n = q.
The corresponding elements of matrices A and B must be equal, i.e., aij = bij for all i and j.
Question 3: How to prove that two matrices are equal?
Answer:
To prove that two matrices are equal, we have to prove that the order of the given matrices is equal, i.e., the same number of rows and columns, and also the corresponding elements are also equal.
Question 4: How can we solve the equality of matrices?
Answer:
Two equal matrices can be solved by comparing their corresponding elements. If there are any unknown variables, then solve them by equating them with the corresponding elements in the other matrix.
Share your thoughts in the comments
Please Login to comment...