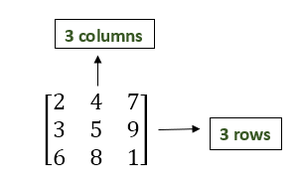
How to Solve a System of Equations using Inverse of Matrices?

Last Updated : 19 Jan, 2022

In mathematics, a matrix is an array of numbers arranged in a rectangular pattern and separated into rows and columns. They’re commonly depicted by enclosing all of the integers within square brackets.

Determinant

A matrix’s determinant is the scalar value produced for a given square matrix. The determinant is dealt with in linear algebra, and it is computed using the elements of a square matrix. A determinant is a scalar value or number calculated using a square matrix. The square matrix might be 2 × 2, 3 × 3, 4 × 4, or any other form where the number of columns and rows are equal, such as n × n. If S is the set of square matrices, R is the set of integers (real or complex), and f: S → R is defined by f (A) = k, where A ∈ S and k ∈ R, then f (A) is referred to as A’s determinant. A determinant is represented by two vertical lines, i.e., |A|.

Determinant of 2×2 matrix –

$\left[\begin{matrix}a&b\\c&d\\\end{matrix}\right] = a ×d - b ×c$

Determinant of 3×3 matrix – $\left[\begin{matrix}a&b&c\\d&e&f\\g&h&i\\\end{matrix}\right]=a(ei-fh)-b(di-gf)+c(dh-ge)$

Minors and Cofactors

The matrix created after eliminating the row and column of the matrix in which that specific element lies is defined as the minor of the matrix.

The minor of the element a₁₂is M₁₂ – $\left[\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right]=\left[\begin{matrix}a_{21}&a_{23}\\a_{31}&a_{33}\\\end{matrix}\right]$

The cofactor of an element in matrix A is produced by multiplying the element’s minor M_ijby (-1)^i+j . C_ijis the symbol for an element’s cofactor. If the minor of a matrix is M_ij, then the cofactor of the element would be: C_{ij =}(-1)^i+j M_{ij .}The cofactor matrix is the matrix created by the cofactors of the matrix’s components.

Cofactor Matrix : $\left[\begin{matrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{33}\\\end{matrix}\right]$

Adjoint of a matrix

Let A=[aij] be an n-dimensional square matrix. A matrix A’s adjoint is the transpose of A’s cofactor matrix. It is symbolized by the letter adj A. Adjoint matrices are sometimes known as adjugate matrices. The adjoint of a square matrix A = [aij]n x n is defined as the transpose of the matrix [Aij]n x n, where Aij is the cofactor of the element aij.

$Let A = \left[\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right]$

Adjoint of A=Transpose of $\left[\begin{matrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\\\end{matrix}\right]$ = $\left[\begin{matrix}A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23}&A_{33}\\\end{matrix}\right]$

The inverse of a matrix

A square matrix A is invertible if and only if A is a nonsingular matrix. The inverse of a matrix may be obtained by dividing the adjoint of a matrix by the determinant of the matrix. The inverse of a matrix may be computed by following the steps below:

Step 1: Determine the minor of the provided matrix.
Step 2: Convert the acquired matrix into the cofactors matrix.
Step 3: Finally, the adjugate, and
Step 4: Multiply it by the determinant’s reciprocal.

Let A= $\left[\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right]$

Inverse of matrix A = A^{-1} = $\frac{1}{|A|} \left[\begin{matrix}A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23}&A_{33}\\\end{matrix}\right]$

Application of Matrices and Determinants

Now, let’s look at how determinants and matrices may be used to solve systems of linear equations in two or three variables and to assess the system’s consistency.

Consistent System: A system of equations is considered to be consistent if it has (one or more) solutions.
Inconsistent System: If the solution to a system of equations does not exist, the system is said to be inconsistent.

Representing linear systems with matrix equations

An augmented matrix can be used to represent a system of equations. Each row in an augmented matrix represents one of the system’s equations, while each column represents a variable or the constant terms. We can see that augmented matrices are a shortcut for formulating systems of equations in this way.

Example: Write the following system of equations as an augmented matrix.

x – 2y = 5

4x – 3y – z = 3

5y – 7z = 9

Let’s write the following matrix in augmented form. If a variable term is not given in the matrix, it is considered that the coefficient of that term is ‘ 0 ‘.

(1)x + (-2)y + (0)z = 5

(4)x + (-3)y + (-1)z = 3

(0)x + (5)y + (-7)z = 9

The following augmented matrix is: $\left[\begin{matrix}1&-2&0&5\\4&-3&-1&3\\0&5&-7&9\\\end{matrix}\right]$

Solving linear systems with matrix equations

Solving linear equations using a matrix is done by the Matrix method. In this article, we will look at solving linear equations with matrix examples.

Solving equations with inverse matrices

Let’s suppose the equation is: 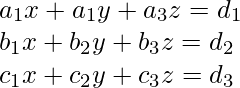$a_1x+a_1y+a_3z=d_1 \\b_1x+b_2y+b_3z=d_2\\ c_1x+c_2y+c_3z=d_3$

Matrix Method is used to find the solution of the system of the equations. In the equations, all of the variables should be written in the proper order. On the appropriate sides, write the variables, their coefficients, and constants.

The method of determining the inverse is used to solve a system of linear equations, and it requires two additional matrices. The variables are represented by Matrix X. The constants are represented by Matrix B. Using matrix multiplication, a system of equations with the same number of equations as a variable is defined as,

AX=B

Let A be the coefficient matrix, X be the variable matrix, and B be the constant matrix to solve a system of linear equations with an inverse matrix. As a result, we’d want to solve the system AX = B. Take a look at the equations below as an example.

$\left[\begin{matrix}a_1x+a_2y+a_3z\\b_1x+b_2y+b_3z\\c_1x+c_2y+c_3z\\\end{matrix}\right]=\left[\begin{matrix}d_1\\d_2\\d_3\\\end{matrix}\right]$

$\left[\begin{matrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\\\end{matrix}\right]\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\left[\begin{matrix}d_1\\d_2\\d_3\\\end{matrix}\right]$

AX = B

where: $A=\left[\begin{matrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right],B=\left[\begin{matrix}d_1\\d_2\\d_3\\\end{matrix}\right]$

Case 1: If A is a nonsingular matrix, it has an inverse.

Let A be the coefficient matrix, X be the variable matrix, and B be the constant matrix to solve a system of linear equations with an inverse matrix. As a result, we’d want to solve the system AX=B. To get the answer, multiply both sides by the inverse of A.

$(A^{-1})AX=(A^{-1})B [(A^{-1})A]X=(A^{-1})B IX=(A^{-1})B X=(A^{-1})B$

As the inverse of a matrix is unique, this matrix equation offers a unique solution to the given system of equations. The Matrix Method is a method for solving systems of equations.

Case 2: If A is a singular matrix, then | A| = 0. In this case, calculate (adj A) B.

If (adj A) B ≠ O, (O being zero matrices), then the solution does not exist and the system of equations is called inconsistent.

If (adj A) B = O, then the system may be either consistent or inconsistent accordingly as the system has either infinitely many solutions or no solution.

Sample Problems

Question 1: Find the following of the given matrix $A=\left[\begin{matrix}3&2&-1\\-5&0&-2\\3&4&-1\\\end{matrix}\right]$

determinant of matrix A
cofactor matrix A
adjoint of matrix A
inverse of matrix A

Solution:

The given matrix is $A=\left[\begin{matrix}3&2&-1\\-5&0&-2\\3&4&-1\\\end{matrix}\right]$

Determinant of the A = $3(0\times (-1) - 4\times(-2))+5(2\times(-1)-4\times(-1))+3(2\times(-2)-0\times (-1))$

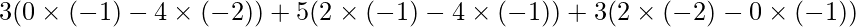
= 3(0+8)+5(-2+4)+3(-4)

= 3 × 8 + 5 × 2 + 3 × (-4)

= 24 + 10 – 12 units

Cofactor of matrix A =

C₁₁ = 0 × (-1) -4 × (-2) = 0 + 8 = 8

C₁₂= -((-5) × (-1) -3 × (-2)) = -(5 + 6) = -11

C₁₃= (-5) × 4 -3 × 0 = -20

C₂₁= −(2 × (-1) -4 × (-1)) = -(-2 + 4) = -2

C₂₂= 3 × (-1) -3 × (-1) = -3 + 3 = 0

C₂₃= -(3 × 4 – 3 × 2) = -(12 – 6) = -6

C₃₁ = 2 × (-2) – 0 × (-1) = -4

C₃₂= -(3 × (-2) – (-5) × (-1)) = -(-6 – 5) = 11

C₃₃= 3 × 0 – (-5) × 2 = 10

Cofactor matrix of A = $C=\left[\begin{matrix}8&-11&-20\\-2&0&-6\\-4&11&10\\\end{matrix}\right]$

AdjoinT of matrix A = transpose of cofactor matrix C = $C=\left[\begin{matrix}8&-11&-20\\-2&0&-6\\-4&11&10\\\end{matrix}\right]^{'}$

$C=\left[\begin{matrix}8&-2&-4\\-11&0&11\\-20&-6&10\\\end{matrix}\right]$

Inverse of matrix A = $A^{-1}=\frac{1}{|A|}adj.A$

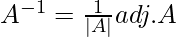
= $\frac{1}{22} \left[\begin{matrix}8&-2&-4\\-11&0&11\\-20&-6&10\\\end{matrix}\right]$

= $\left[\begin{matrix}\frac{4}{11}&\frac{-1}{11}&\frac{-2}{11}\\\frac{-1}{2}&0&\frac{1}{2}\\\frac{-10}{11}&\frac{-3}{11}&\frac{5}{11}\\\end{matrix}\right]$

Question 2: Ram is hired for a job with a monthly payment of a specific amount and an annual increase of a predetermined amount. Find his beginning pay and yearly increase if his salary was $300 per month at the end of the first month after 1 year of service and $600 per month at the end of the first month after 3 years of service.

Solution:

Let “x” and “y” represent the monthly salary and a yearly increase of a certain amount, respectively.

According to the question;

x + y = 300 ⇢ (i)

x + 3y = 600 ⇢ (ii)

This can be written as AX = B, where

$A=\left[\begin{matrix}1&1\\1&3\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\\end{matrix}\right] ,B=\left[\begin{matrix}300\\600\\\end{matrix}\right]$

Determinant of A = 1 × 3 – 1 × 1 = 3 – 1 = 2

Adjoin of A = $\left[\begin{matrix}3&-1\\-1&1\\\end{matrix}\right]$

Thus, $A^{-1}=\frac{1}{|A|}adj.A$

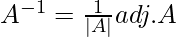
$A^{-1}=\frac{1}{2}\left[\begin{matrix}3&-1\\-1&1\\\end{matrix}\right]$

Using Matrix Inverse,

X = A^-1B

$X= \frac{1}{2} \left[\begin{matrix}3&-1\\-1&1\\\end{matrix}\right]\left[\begin{matrix}300\\600\\\end{matrix}\right]$

$X=\frac{1}{2} \left[\begin{matrix}3\times300+(-1)\times600\\(-1)\times300+1\times600\\\end{matrix}\right]$

$X= \frac{1}{2} \left[\begin{matrix}300\\300\\\end{matrix}\right]$

$X=\left[\begin{matrix}150\\150\\\end{matrix}\right]$

Therefore; x = $150, y = $150

So, the monthly salary is $150 and the annual increment is $150.

Question 3: The sum of three numbers is 3. If we multiple the second number by 2 and add the first number to it, we get 6. If we multiply the third number by 4 and add the second number to it, we get 10. Represent it algebraically and find the numbers using the matrix method.

Solution:

Let x, y, and z represent the first, second, and third numbers, respectively. Then, according to the question, we have

x + y + z = 3

x + 2y = 6

y + 4z = 10

This can be written as AX = B, where $A=\left[\begin{matrix}1&1&1\\1&2&0\\0&1&4\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right] ,B=\left[\begin{matrix}3\\10\\6\\\end{matrix}\right]$

Here, |A|= 1(8 – 0) – 1(4 – 0) + 1(1 – 0) = 8 – 4 + 1 = 5 ≠ 0. Now, find adj A.

A₁₁= 8 – 0 = 8, A₁₂= -(4 – 0) = -4, A₁₃= 1 – 0 = 1

A₂₁= -(4 – 1) = -3, A₂₂= 4 – 0 = 4, A₂₃= -(1 – 0) = -1

A₃₁= 0 – 2 = -2, A₃₂ = -(0 – 1) = 1, A₃₃ = 2 – 1 = 1

Adj. A = $\left[\begin{matrix}8&-3&-2\\-4&4&1\\1&-1&1\\\end{matrix}\right]$

Thus, $A^{-1}=\frac{1}{|A|}Adj. of A=\frac{1}{5}\left[\begin{matrix}8&-3&-2\\-4&4&1\\1&-1&1\\\end{matrix}\right]$

X = A^-1B

$X=\frac{1}{5}\left[\begin{matrix}8&-3&-2\\-4&4&1\\1&-1&1\\\end{matrix}\right]\left[\begin{matrix}3\\10\\6\\\end{matrix}\right]$

$\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\frac{1}{5}\left[\begin{matrix}24-30-12\\-12+40+6\\3-10+6\\\end{matrix}\right]=\frac{1}{5}\left[\begin{matrix}-18\\34\\-1\\\end{matrix}\right]=\left[\begin{matrix}\frac{-18}{5}\\\frac{34}{5}\\\frac{-1}{5}\\\end{matrix}\right]$

Therefore;

$X=\frac{-18}{5}, Y= \frac{34}{5}, Z=\frac{-1}{5}$

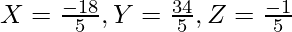
Question 4: Assume Joe, Max, and Polly went shopping at the mall. Joe pays 45/- for 4 kg of apples, 7 kg of bananas, and 6 kg of guavas, Max pays 30/- for 2 kg of apples and 5 kg of guavas, and Polly pays 35/- for 3 kg of apples, 1 kg of bananas, and 4 kg of guavas. How much do apples, bananas, and guavas cost per kilogram?

Solution:

Let x, y, and z represent the number of apples, bananas, and guavas, respectively.

In accordance to the question:

4x + 7y + 6z = 45

2 x + 5 z = 30

3x + y + 4z = 35

Matrix A contains the kg of apples, bananas, and guavas bought by Joe, Max, and Polly. Matrix B contains the prices paid by the three and matrix X contains the variables.

$A=\left[\begin{matrix}4&7&6\\2&0&5\\3&1&4\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right] ,B=\left[\begin{matrix}45\\30\\35\\\end{matrix}\right]$

The solution of the given system of equations be X = A^-1 B.

In order to find the inverse of A, we will first find the determinant of A.

$A=\left[\begin{matrix}4&7&6\\2&0&5\\3&1&4\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right] ,B=\left[\begin{matrix}45\\30\\35\\\end{matrix}\right]$

$A^{-1}=\frac{1}{|A|}adj. A$

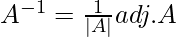
Determinant of A = |A| = 4(0 × 4 – 1 × 5) – 7(2 × 4 – 5 × 3) + 6(2 × 1 – 3 × 0)

= 4(0 – 5) – 7(8 – 15) + 6(2 – 0)

= -20 – 7(-7) + 12

= -20 + 49 + 12 = 41

Adj. of A = $\left[\begin{matrix}-5&-22&35\\7&-2&-6\\2&17&-14\\\end{matrix}\right]$

$A^{-1}=\frac{1}{41}adj.A$

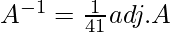
$X=A^{-1}B=\frac{1}{41}\left[\begin{matrix}-5&-22&35\\7&-2&-6\\2&17&-14\\\end{matrix}\right]\times \left[\begin{matrix}45\\30\\35\\\end{matrix}\right]$

$X=\frac{1}{41}\left[\begin{matrix}340\\45\\110\\\end{matrix}\right]=\left[\begin{matrix}8.3\\1.1\\2.7\\\end{matrix}\right]$

The cost of apples per kg = 8.3/-

The cost of bananas per kg = 1.1/-

The cost of guavas per kg = 2.7/-

Question 5: The cost of 2 kg potatoes, 3 kg tomatoes, and 2 kg flour is 50. The cost of 5 kg potatoes, 1 kg tomatoes and 6 kg flour is 40. The cost of 4 kg potatoes, 6 kg tomatoes and 3 kg flour is 60. Find the cost of each item per kg by the inverse of a matrix.

Solution:

Let x, y, and z represent the kg of potatoes, tomatoes, and flour, respectively.

In accordance to the question:

2x + 3y + 2z = 50

5x + 1y + 6z = 40

4x + 6y + 3z = 60

Matrix A contains the kg of potatoes, tomatoes and flour. Matrix B contains the prices paid and matrix X contains the variables. This can be written as AX = B, where $A=\left[\begin{matrix}2&3&2\\5&1&6\\4&6&3\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right] ,B=\left[\begin{matrix}50\\40\\60\\\end{matrix}\right]$

The solution of the given system of equations is X = A^-1B. In order to find the inverse of A, we will first find the determinant of A.

Determinant of A |A| = 2(3 – 36) – 3(15 – 24) + 2(30 – 4) = 2 × (-33) – 3(-9) + 2(26) = -66 + 27 + 52 = 13

Now, find the adjoint of A to get the inverse of A.

A₁₁= 3 – 36 = -33, A₁₂= -(15 – 24) = 9, A₁₃= 30 – 4 = 26

A₂₁= -(9 – 12) = 3, A₂₂= 6 – 8 = -2, A₂₃= -(12 – 12) = 0

A^{-1}= $A^{-1}=\frac{1}{|A|}adj.A=\frac{1}{13}\left[\begin{matrix}-33&3&16\\9&-2&-2\\26&0&-13\\\end{matrix}\right]$

A₃₁= 18 – 2 = 16, A₃₂= -(12 – 10) = -2, A₃₃= 2 – 15 = -13

Thus, $Adj. A=\left[\begin{matrix}-33&3&16\\9&-2&-2\\26&0&-13\\\end{matrix}\right]$

X = A^-1B

$X=\frac{1}{13}\left[\begin{matrix}-33&3&16\\9&-2&-2\\26&0&-13\\\end{matrix}\right]\left[\begin{matrix}50\\40\\60\\\end{matrix}\right]$

$\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\frac{1}{13}\left[\begin{matrix}-33\times50+3\times40+16\times 60\\9\times 50-2\times 40-2\times 60\\26\times 50+0\times 40-13\times 60\\\end{matrix}\right]=\frac{1}{13}\left[\begin{matrix}-570\\250\\520\\\end{matrix}\right]=\left[\begin{matrix}-43.8\\19.2\\40\\\end{matrix}\right]$

x = 43.8, y = 19.2, z = 40