Graph Plotting in Python | Set 3

Matplotlib is a pretty extensive library which supports Animations of graphs as well. The animation tools center around the matplotlib.animation base class, which provides a framework around which the animation functionality is built. The main interfaces are TimedAnimation and FuncAnimation and out of the two, FuncAnimation is the most convenient one to use.

Installation:

Matplotlib: Refer to Graph Plotting in Python | Set 1
Numpy: You can install numpy module using following pip command:
```
pip install numpy
```
FFMPEG: It is required only for saving the animation as a video. The executable can be downloaded from here.

Implementation:

# importing required modules
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
  
# create a figure, axis and plot element
fig = plt.figure()
ax = plt.axes(xlim=(-50, 50), ylim=(-50, 50))
line, = ax.plot([], [], lw=2)
  
# initialization function
def init():
    # creating an empty plot/frame
    line.set_data([], [])
    return line,
  
# lists to store x and y axis points
xdata, ydata = [], []
  
# animation function
def animate(i):
    # t is a parameter
    t = 0.1*i
      
    # x, y values to be plotted
    x = t*np.sin(t)
    y = t*np.cos(t)
      
    # appending new points to x, y axes points list
    xdata.append(x)
    ydata.append(y)
      
    # set/update the x and y axes data
    line.set_data(xdata, ydata)
      
    # return line object
    return line,
      
# setting a title for the plot
plt.title('A growing coil!')
# hiding the axis details
plt.axis('off')
  
# call the animator    
anim = animation.FuncAnimation(fig, animate, init_func=init,
                               frames=500, interval=20, blit=True)
  
# save the animation as mp4 video file
anim.save('animated_coil.mp4', writer = 'ffmpeg', fps = 30)
  
# show the plot
plt.show()

Here is how the output animation looks like:

Now, let us try to understand the code in pieces:

```
fig = plt.figure()
ax = plt.axes(xlim=(-50, 50), ylim=(-50, 50))
line, = ax.plot([], [], lw=2)
```
Here, we first create a figure, i.e a top level container for all our subplots.
Then we create an axes element ax which acts as a subplot. The range/limit for x and y axis are also defined while creating the axes element.
Finally, we create the plot element, named as line . Initially, the x and y axis points have been defined as empty lists and line-width (lw) has been set as 2.
```
def init():
    line.set_data([], [])
    return line,
```
Now, we declare a initialization function, init . This function is called by animator to create the first frame.
```
def animate(i):
    # t is a parameter
    t = 0.1*i
    
    # x, y values to be plotted
    x = t*np.sin(t)
    y = t*np.cos(t)
    
    # appending new points to x, y axes points list
    xdata.append(x)
    ydata.append(y)
    
    # set/update the x and y axes data
    line.set_data(xdata, ydata)
    
    # return line object
    return line,
```
This is the most important function of above program. animate() function is called again and again by the animator to create each frame. The number of times this function will be called is determined by number of frames, which is passed as frames argument to animator.
animate() function takes the index of ith frame as argument.
```
t = 0.1*i
```
Here, we cleverly use the index of current frame as a parameter!
```
x = t*np.sin(t)
y = t*np.cos(t)
```
Now, since we have the parameter t, we can easily plot any parametric equation. For example, here, we are plotting a spiral using its parametric equation.
```
line.set_data(xdata, ydata)
return line,
```
Finally, we use set_data() function to set x and y data and then return plot object, line .
```
anim = animation.FuncAnimation(fig, animate, init_func=init,
                               frames=500, interval=20, blit=True)
```
Now, we create the FuncAnimation object, anim . It takes various arguments explained below:
fig : figure to be plotted.
animate : the function to be called repeatedly for each frame.
init_func : function used to draw a clear frame. It is called once before the first frame.
frames : number of frames. (Note: frames can also be an iterable or generator.)
interval : duration between frames ( in milliseconds)
blit : setting blit=True means that only those parts will be drawn, which have changed.
```
anim.save('animated_coil.mp4', writer = 'ffmpeg', fps = 30)
```
Now, we save the animator object as a video file using save() function. You will need a movie writer for saving the animation video. In this example, we have used FFMPEG movie writer. So, writer is set as ‘ffmpeg’.
fps stands for frame per second.

Example 2

This example shows how one can make a rotating curve by applying some simple mathematics!

# importing required modules
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
  
# create a figure, axis and plot element
fig = plt.figure()
ax = plt.axes(xlim=(-25, 25), ylim=(-25, 25))
line, = ax.plot([], [], lw=2)
  
# initialization function
def init():
    # creating an empty plot/frame
    line.set_data([], [])
    return line,
  
# set of points for a star (could be any curve)
p = np.arange(0, 4*np.pi, 0.1)
x = 12*np.cos(p) + 8*np.cos(1.5*p)
y = 12*np.sin(p) - 8*np.sin(1.5*p)
  
# animation function
def animate(i):
    # t is a parameter
    t = 0.1*i
      
    # x, y values to be plotted
    X = x*np.cos(t) - y*np.sin(t)
    Y = y*np.cos(t) + x*np.sin(t)
      
    # set/update the x and y axes data
    line.set_data(X, Y)
      
    # return line object
    return line,
      
# setting a title for the plot
plt.title('A rotating star!')
# hiding the axis details
plt.axis('off')
  
# call the animator    
anim = animation.FuncAnimation(fig, animate, init_func=init,
                               frames=100, interval=100, blit=True)
  
# save the animation as mp4 video file
anim.save('basic_animation.mp4', writer = 'ffmpeg', fps = 10)
  
# show the plot
plt.show()

Here is how the output of above program looks like:

Here, we have used some simple mathematics to rotate a given curve.

The star shape is obtained by putting k = 2.5 and 0<t<4*pi in the parametric equation given below:
$x= [a-b]\cos (t) + b\cos [t(\frac{a}{b}-1)]$
$y= [a-b]\sin (t) - b\sin [t(\frac{a}{b}-1)] , k= \frac{a}{b}$
The same has been applied here:
```
p = np.arange(0, 4*np.pi, 0.1)
x = 12*np.cos(p) + 8*np.cos(1.5*p)
y = 12*np.sin(p) - 8*np.sin(1.5*p)
```
Now, in each frame, we rotate the star curve using concept of rotation in complex numbers. Let x, y be two ordinates. Then after rotation by angle theta, the new ordinates are:
${x}' = x\cos \theta - y\sin \theta$
${y}' = x\sin \theta + y\cos \theta$
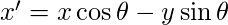
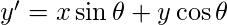The same has been applied here:
```
X = x*np.cos(t) - y*np.sin(t)
Y = y*np.cos(t) + x*np.sin(t)
```

All in all, animations are a great tool to create amazing stuff and many more things can be created using them.

So, this was how animated plots can be generated and saved using Matplotlib.

This article is contributed by Nikhil Kumar. If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Last Updated : 09 Feb, 2018