Graph Plotting in Python | Set 1
Subplots
Subplots are required when we want to show two or more plots in same figure. We can do it in two ways using two slightly different methods.
Method 1
Python
import matplotlib.pyplot as plt
import numpy as np
def create_plot(ptype):
x = np.arange(-10, 10, 0.01)
if ptype == 'linear':
y = x
elif ptype == 'quadratic':
y = x**2
elif ptype == 'cubic':
y = x**3
elif ptype == 'quartic':
y = x**4
return(x, y)
plt.style.use('fivethirtyeight')
fig = plt.figure()
plt1 = fig.add_subplot(221)
plt2 = fig.add_subplot(222)
plt3 = fig.add_subplot(223)
plt4 = fig.add_subplot(224)
x, y = create_plot('linear')
plt1.plot(x, y, color ='r')
plt1.set_title('$y_1 = x$')
x, y = create_plot('quadratic')
plt2.plot(x, y, color ='b')
plt2.set_title('$y_2 = x^2$')
x, y = create_plot('cubic')
plt3.plot(x, y, color ='g')
plt3.set_title('$y_3 = x^3$')
x, y = create_plot('quartic')
plt4.plot(x, y, color ='k')
plt4.set_title('$y_4 = x^4$')
fig.subplots_adjust(hspace=.5,wspace=0.5)
plt.show()
|
Output:

Let us go through this program step by step:
plt.style.use('fivethirtyeight')
- The styling of plots can be configured by setting different styles available or setting your own. You can learn more about this feature here
fig = plt.figure()
- Figure acts as a top level container for all plot elements. So, we define a figure as fig which will contain all our subplots.
plt1 = fig.add_subplot(221)
plt2 = fig.add_subplot(222)
plt3 = fig.add_subplot(223)
plt4 = fig.add_subplot(224)
- Here we use fig.add_subplot method to define subplots and their positions. The function prototype is like this:
add_subplot(nrows, ncols, plot_number)
- If a subplot is applied to a figure, the figure will be notionally split into ‘nrows’ * ‘ncols’ sub-axes. The parameter ‘plot_number’ identifies the subplot that the function call has to create. ‘plot_number’ can range from 1 to a maximum of ‘nrows’ * ‘ncols’.
If the values of the three parameters are less than 10, the function subplot can be called with one int parameter, where the hundreds represent ‘nrows’, the tens represent ‘ncols’ and the units represent ‘plot_number’. This means: Instead of subplot(2, 3, 4) we can write subplot(234).
This figure will make it clear that how positions are specified:

x, y = create_plot('linear')
plt1.plot(x, y, color ='r')
plt1.set_title('$y_1 = x$')
- Next, we plot our points on each subplot. First, we generate x and y axis coordinates using create_plot function by specifying the type of curve we want.
Then, we plot those points on our subplot using .plot method. Title of subplot is set by using set_title method. Using $ at starting and end of the title text will ensure that ‘_'(underscore) is read as a subscript and ‘^’ is read as a superscript.
fig.subplots_adjust(hspace=.5,wspace=0.5)
- This is another utility method which creates space between subplots.
plt.show()
- In the end, we call plt.show() method which will show the current figure.
Method 2
Python
import matplotlib.pyplot as plt
import numpy as np
def create_plot(ptype):
x = np.arange(0, 5, 0.01)
if ptype == 'sin':
y = np.sin(2*np.pi*x)
elif ptype == 'exp':
y = np.exp(-x)
elif ptype == 'hybrid':
y = (np.sin(2*np.pi*x))*(np.exp(-x))
return(x, y)
plt.style.use('ggplot')
plt1 = plt.subplot2grid((11,1), (0,0), rowspan = 3, colspan = 1)
plt2 = plt.subplot2grid((11,1), (4,0), rowspan = 3, colspan = 1)
plt3 = plt.subplot2grid((11,1), (8,0), rowspan = 3, colspan = 1)
x, y = create_plot('sin')
plt1.plot(x, y, label = 'sine wave', color ='b')
x, y = create_plot('exp')
plt2.plot(x, y, label = 'negative exponential', color = 'r')
x, y = create_plot('hybrid')
plt3.plot(x, y, label = 'damped sine wave', color = 'g')
plt1.legend()
plt2.legend()
plt3.legend()
plt.show()
|
Output:
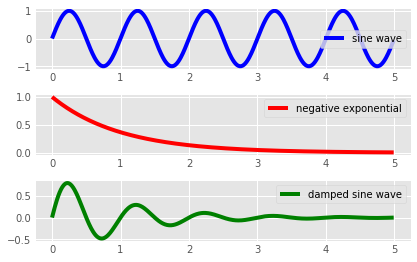
Let us go through important parts of this program as well:
plt1 = plt.subplot2grid((11,1), (0,0), rowspan = 3, colspan = 1)
plt2 = plt.subplot2grid((11,1), (4,0), rowspan = 3, colspan = 1)
plt3 = plt.subplot2grid((11,1), (8,0), rowspan = 3, colspan = 1)
- subplot2grid is similar to “pyplot.subplot” but uses 0-based indexing and let subplot to occupy multiple cells.
Let us try to understand the arguments of the subplot2grid method:
1. argument 1 : geometry of the grid
2. argument 2: location of the subplot in the grid
3. argument 3: (rowspan) No. of rows covered by subplot.
4. argument 4: (colspan) No. of columns covered by subplot.
This figure will make this concept more clear:

- In our example, each subplot spans over 3 rows and 1 column with two empty rows (row no. 4,8) .
x, y = create_plot('sin')
plt1.plot(x, y, label = 'sine wave', color ='b')
- Nothing special in this part as the syntax to plot points on a subplot remains same.
plt1.legend()
- This will show the label of the subplot on the figure.
plt.show()
- Finally, we call the plt.show() function to show the current plot.
Note: After going through the above two examples, we can infer that one should use subplot() method when the plots are of uniform size where as subplot2grid() method should be preferred when we want more flexibility on position and sizes of our subplots.
3-D plotting
We can easily plot 3-D figures in matplotlib. Now, we discuss some important and commonly used 3-D plots.
Python
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
fig = plt.figure()
ax1 = fig.add_subplot(111, projection='3d')
x = np.random.randint(0, 10, size = 20)
y = np.random.randint(0, 10, size = 20)
z = np.random.randint(0, 10, size = 20)
ax1.set_xlabel('x-axis')
ax1.set_ylabel('y-axis')
ax1.set_zlabel('z-axis')
plt.show()
|
- Output of above program will provide you with a window which can rotate or enlarge the plot. Here is a screenshot: (dark points are nearer than light ones)

- Let us try to understand some important aspects of this code now.
from mpl_toolkits.mplot3d import axes3d
- This is the module required to plot on 3-D space.
ax1 = fig.add_subplot(111, projection='3d')
- Here, we create a subplot on our figure and set projection argument as 3d.
ax1.scatter(x, y, z, c = 'm', marker = 'o')
- Now we use .scatter() function to plot the points in XYZ plane.
- Plotting lines
Python
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
fig = plt.figure()
ax1 = fig.add_subplot(111, projection='3d')
x = np.random.randint(0, 10, size = 5)
y = np.random.randint(0, 10, size = 5)
z = np.random.randint(0, 10, size = 5)
ax1.plot_wireframe(x,y,z)
ax1.set_xlabel('x-axis')
ax1.set_ylabel('y-axis')
ax1.set_zlabel('z-axis')
plt.show()
|
- A screenshot of the 3-D plot of above program will look like:

- The main difference in this program with previous one is:
ax1.plot_wireframe(x,y,z)
- We used .plot_wireframe() method to plot lines over a given set of 3-D points.
- Plotting Bars
Python
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
fig = plt.figure()
ax1 = fig.add_subplot(111, projection='3d')
x = [1,2,3,4,5,6,7,8,9,10]
y = [4,3,1,6,5,3,7,5,3,7]
z = np.zeros(10)
dx = np.ones(10)
dy = np.ones(10)
dz = [1,3,4,2,6,7,5,5,10,9]
color = []
for h in dz:
if h > 5:
color.append('r')
else:
color.append('b')
ax1.bar3d(x, y, z, dx, dy, dz, color = color)
ax1.set_xlabel('x-axis')
ax1.set_ylabel('y-axis')
ax1.set_zlabel('z-axis')
plt.show()
|
- A screenshot of the 3-D environment created is here:

- Let us go through important aspects of this program:
x = [1,2,3,4,5,6,7,8,9,10]
y = [4,3,1,6,5,3,7,5,3,7]
z = np.zeros(10)
- Here, we define the base positions of bars. Setting z = 0 means all bars start from XY plane.
dx = np.ones(10) # length along x-axis
dy = np.ones(10) # length along y-axs
dz = [1,3,4,2,6,7,5,5,10,9] # height of bar
- dx, dy, dz denote the size of bar. Consider he bar as a cuboid, then dx, dy, dz are its expansions along x, y, z axis respectively.
for h in dz:
if h > 5:
color.append('r')
else:
color.append('b')
- Here, we set the color for each bar as a list. The color scheme is red for bars with height greater than 5 and blue otherwise.
ax1.bar3d(x, y, z, dx, dy, dz, color = color)
- Finally, to plot the bars, we use .bar3d() function.
- Plotting curves
Python
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
fig = plt.figure()
ax1 = fig.add_subplot(111, projection='3d')
u, v = np.mgrid[0:2*np.pi:200j, 0:np.pi:100j]
x=np.cos(u)*np.sin(v)
y=np.sin(u)*np.sin(v)
z=np.cos(v)
ax1.plot_wireframe(x, y, z, rstride = 5, cstride = 5, linewidth = 1)
plt.show()
|
- Output of this program will look like this:
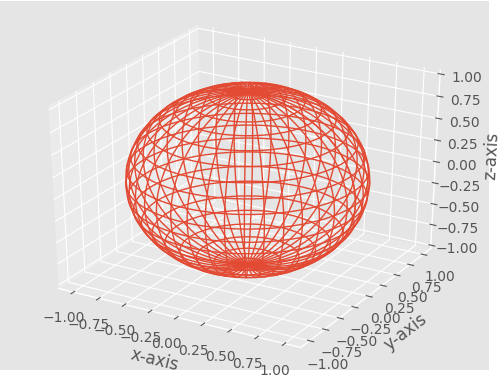
- Here, we plotted a sphere as a mesh grid.
Let us go through some important parts:
u, v = np.mgrid[0:2*np.pi:200j, 0:np.pi:100j]
- We use np.mgrid in order to get points so that we can create a mesh.
You can read more about this here.
x=np.cos(u)*np.sin(v)
y=np.sin(u)*np.sin(v)
z=np.cos(v)
- This is nothing but the parametric equation of a sphere.
ax1.plot_wireframe(x, y, z, rstride = 5, cstride = 5, linewidth = 1)
- Agan, we use .plot_wireframe() method. Here, rstride and cstride arguments can be used to set how much dense our mesh must be.
Next Article: Graph Plotting in Python | Set 3
Share your thoughts in the comments
Please Login to comment...