Getting binomial coefficient of a number in Julia – binomial() Method
The binomial() is an inbuilt function in julia which is used to return the binomial coefficient 
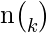
which is the coefficient of the kth term in the polynomial expansion of 
.
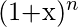
Its formula is –
![\[\binom{n}{k} = \frac{n!}{k! (n-k)!}\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0bcaff88a91ef8c0311e6417d2556c07_l3.png "Rendered by QuickLaTeX.com")
, where 
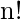
is the factorial of n.
If n is negative, then it is defined in terms of the identity
![\[\binom{n}{k} = (-1)^k \binom{k-n-1}{k}\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8be8baf1e91672558a9b0e057ad6ce12_l3.png "Rendered by QuickLaTeX.com")
.
Syntax: binomial(n::Integer, k::Integer)
Parameters:
- n: Specified number
- k: Specified number
Returns: It returns the binomial coefficient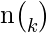
Example 1:
# Julia program to illustrate # the use of binomial() method # Getting the binomial coefficientprintln(binomial(6, 4))println(factorial(6) ÷ (factorial(6-4) * factorial(4))) |
Output:
15 15
Example 2:
# Julia program to illustrate # the use of binomial() method # Getting the binomial coefficientprintln(binomial(6, 3))println(binomial(-6, 3))println(binomial(-6, -2))println(binomial(5, 2)) |
Output:
20 -56 0 10
Please Login to comment...