Generate all cyclic permutations of a number
Last Updated :
07 Jan, 2024
Given a number N, our task is to generate all the possible cyclic permutations of the number.
A cyclic permutation shifts all the elements of a set by a fixed offset. For a set with elements  ,
, 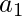 , …,
, …, 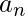 , a cyclic permutation of one place to the left would yield
, a cyclic permutation of one place to the left would yield 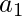 , …,
, …, 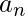 ,
,  , and a cyclic permutation of one place to the right would yield
, and a cyclic permutation of one place to the right would yield 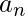 ,
,  ,
, 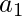 , ….
, ….
Examples:
Input : 123
Output : 123
312
231
Input : 5674
Output : 5674
4567
7456
6745
The idea is to generate next permutation of a number using below formula.
rem = num % 10;
div = num / 10;
num = (pow(10, n - 1)) * rem + div;
While repeating above steps, if we come back to original number, we stop and return.
C++
#include <bits/stdc++.h>
using namespace std;
int countdigits(int N)
{
int count = 0;
while (N) {
count++;
N = N / 10;
}
return count;
}
void cyclic(int N)
{
int num = N;
int n = countdigits(N);
while (1) {
cout << num << endl;
int rem = num % 10;
int div = num / 10;
num = (pow(10, n - 1)) * rem + div;
if (num == N)
break;
}
}
int main()
{
int N = 5674;
cyclic(N);
return 0;
}
|
Java
public class GFG
{
static int countdigits(int N)
{
int count = 0;
while (N>0) {
count++;
N = N / 10;
}
return count;
}
static void cyclic(int N)
{
int num = N;
int n = countdigits(N);
while (true) {
System.out.println(num);
int rem = num % 10;
int dev = num / 10;
num = (int)((Math.pow(10, n - 1)) *
rem + dev);
if (num == N)
break;
}
}
public static void main (String[] args) {
int N = 5674;
cyclic(N);
}
}
|
Python3
import math
def countdigits(N):
count = 0;
while (N):
count = count + 1;
N = int(math.floor(N / 10));
return count;
def cyclic(N):
num = N;
n = countdigits(N);
while (1):
print(int(num));
rem = num % 10;
div = math.floor(num / 10);
num = ((math.pow(10, n - 1)) *
rem + div);
if (num == N):
break;
N = 5674;
cyclic(N);
|
C#
using System;
class GFG
{
static int countdigits(int N)
{
int count = 0;
while (N > 0) {
count++;
N = N / 10;
}
return count;
}
static void cyclic(int N)
{
int num = N;
int n = countdigits(N);
while (true) {
Console.WriteLine(num);
int rem = num % 10;
int dev = num / 10;
num = (int)((Math.Pow(10, n - 1)) *
rem + dev);
if (num == N)
break;
}
}
public static void Main ()
{
int N = 5674;
cyclic(N);
}
}
|
PHP
<?php
function countdigits($N)
{
$count = 0;
while ($N)
{
$count++;
$N = floor($N / 10);
}
return $count;
}
function cyclic($N)
{
$num = $N;
$n = countdigits($N);
while (1)
{
echo ($num);
echo "\n" ;
$rem = $num % 10;
$div = floor($num / 10);
$num = (pow(10, $n - 1)) * $rem + $div;
if ($num == $N)
break;
}
}
$N = 5674;
cyclic($N);
?>
|
Javascript
<script>
function countdigits(N)
{
var count = 0;
while (N>0) {
count++;
N = parseInt(N / 10);
}
return count;
}
function cyclic(N)
{
var num = N;
var n = countdigits(N);
while (true) {
document.write(num+"<br>");
var rem = num % 10;
var dev = parseInt(num / 10);
num = parseInt(((Math.pow(10, n - 1)) *
rem + dev));
if (num == N)
break;
}
}
var N = 5674;
cyclic(N);
</script>
|
Output5674
4567
7456
6745
Time Complexity: O(N), where N is the number of digits
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...