Sum of digit of a number using recursion
Last Updated :
16 Jun, 2022
Given a number, we need to find sum of its digits using recursion.
Examples:
Input : 12345
Output : 15
Input : 45632
Output :20
The step-by-step process for a better understanding of how the algorithm works.
Let the number be 12345.
Step 1-> 12345 % 10 which is equal-too 5 + ( send 12345/10 to next step )
Step 2-> 1234 % 10 which is equal-too 4 + ( send 1234/10 to next step )
Step 3-> 123 % 10 which is equal-too 3 + ( send 123/10 to next step )
Step 4-> 12 % 10 which is equal-too 2 + ( send 12/10 to next step )
Step 5-> 1 % 10 which is equal-too 1 + ( send 1/10 to next step )
Step 6-> 0 algorithm stops
following diagram will illustrate the process of recursion
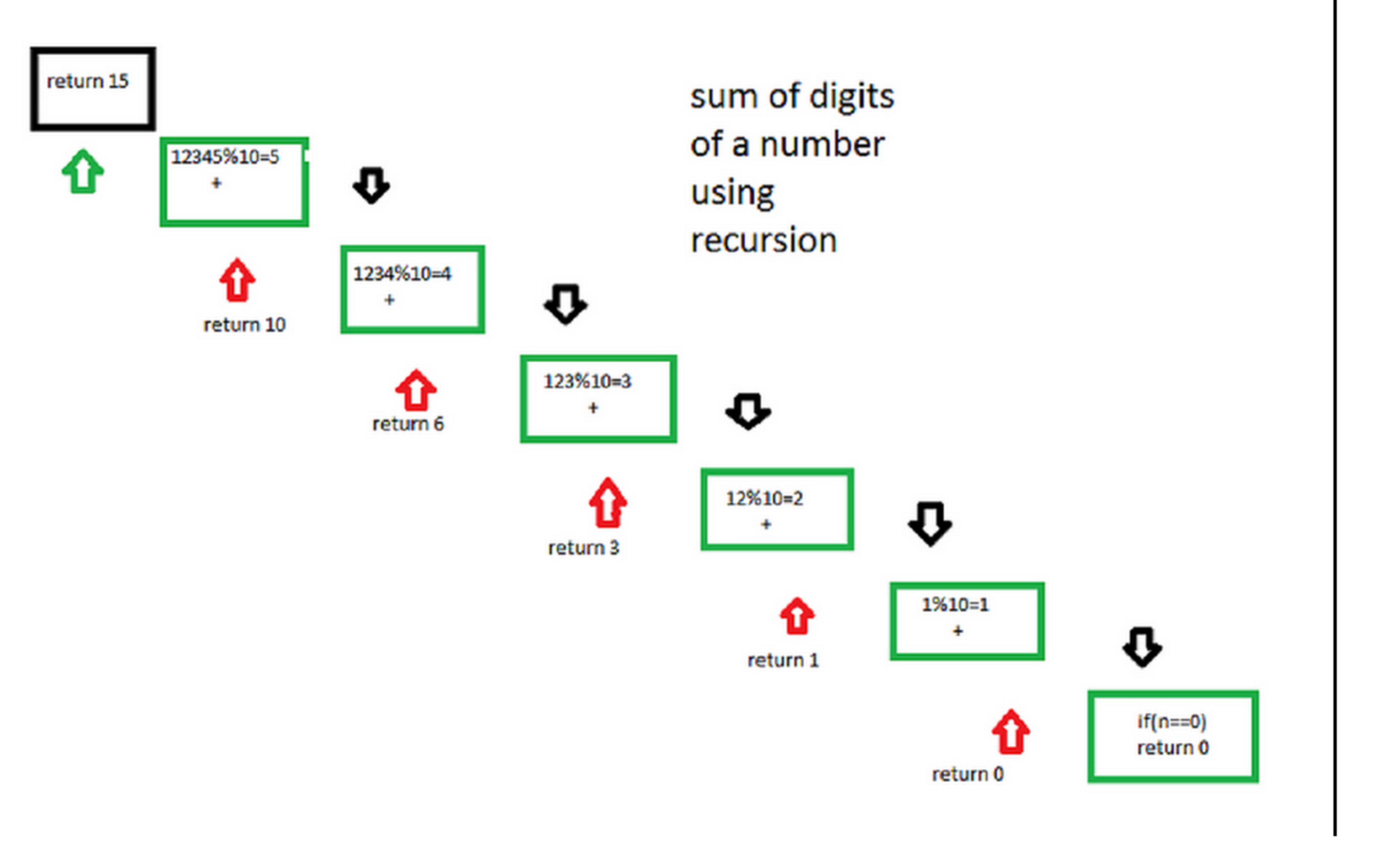
C++
#include <bits/stdc++.h>
using namespace std;
int sum_of_digit(int n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(n / 10));
}
int main()
{
int num = 12345;
int result = sum_of_digit(num);
cout << "Sum of digits in "<< num
<<" is "<<result << endl;
return 0;
}
|
C
#include <stdio.h>
int sum_of_digit(int n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(n / 10));
}
int main()
{
int num = 12345;
int result = sum_of_digit(num);
printf("Sum of digits in %d is %d\n", num, result);
return 0;
}
|
Java
import java.io.*;
class sum_of_digits
{
static int sum_of_digit(int n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(n / 10));
}
public static void main(String args[])
{
int num = 12345;
int result = sum_of_digit(num);
System.out.println("Sum of digits in " +
num + " is " + result);
}
}
|
Python3
def sum_of_digit( n ):
if n == 0:
return 0
return (n % 10 + sum_of_digit(int(n / 10)))
num = 12345
result = sum_of_digit(num)
print("Sum of digits in",num,"is", result)
|
C#
using System;
class GFG {
static int sum_of_digit(int n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(n / 10));
}
public static void Main()
{
int num = 12345;
int result = sum_of_digit(num);
Console.WriteLine("Sum of digits in " +
num + " is " + result);
}
}
|
PHP
<?php
function sum_of_digit($n)
{
if ($n == 0)
return 0;
return ($n % 10 +
sum_of_digit($n / 10));
}
$num = 12345;
$result = sum_of_digit($num);
echo("Sum of digits in " . $num . " is " . $result);
?>
|
Javascript
<script>
function sum_of_digit(n)
{
if (n == 0)
return 0;
return (n % 10 + sum_of_digit(parseInt(n / 10)));
}
var num = 12345;
var result = sum_of_digit(num);
document.write( "Sum of digits in "+ num
+" is "+result );
</script>
|
Output:
Sum of digits in 12345 is 15
Besides writing (n==0 , then return 0) in the code given above we can also write it in this manner , there will be no change in the output .
if(n<10) return n; By writing this there will be no need to call the function for the numbers which are less than 10
Time complexity : O(logn) where n is the given number.
Auxiliary space : O(logn) due to recursive stack space.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...