Game Theory (Normal-form game) | Set 3 (Game with Mixed Strategy)
Last Updated :
02 Aug, 2019
Consider the following payoff matrix with respect to player A and solve it optimally.

Solution:
If a game has no saddle point then the game is said to have mixed strategy.
- Step 1: Find out the row minimum and column maximum.
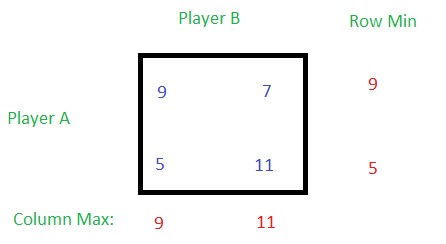
- Step 2: Find out the minimax and maximin values.

Since minimax and maximin value of this game are not equal, this game has no saddle point.
-
Step 3: Now take the 2×2 matrix and find out the oddments for both row and column.
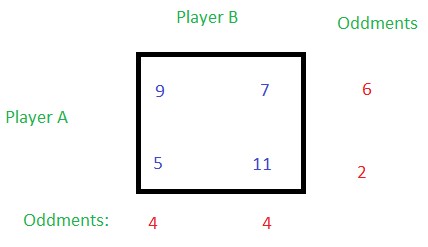
Oddments: Take the difference between the highest outcome and the smallest outcome of the first row and put it at the right side of the second row (see the figure above), i.e. the difference between 9 and 7 is 2, and it is placed at the right of the second row. Similarly, take the difference between highest and the lowest outcome in the second row and put it at the right of the first row, i.e. the difference between 11 and 5 is 6, and is placed at the right of the first row. Similarly, find oddments for columns as well. Take the difference between the greater and the smaller outcome of one column and place it at the bottom of the other column. 11 – 7 = 4 is placed at the bottom of the first column while 9 – 5 = 4 is placed at the bottom of the second column.
-
Step 4: Now find the probabilities for each row.
Using Formula

Let x and (1 – x) be the probabilities of selection of strategies of player A, and y and (1 – y) be the probabilities of selection of strategies of player B, then

And,

Without using Formula
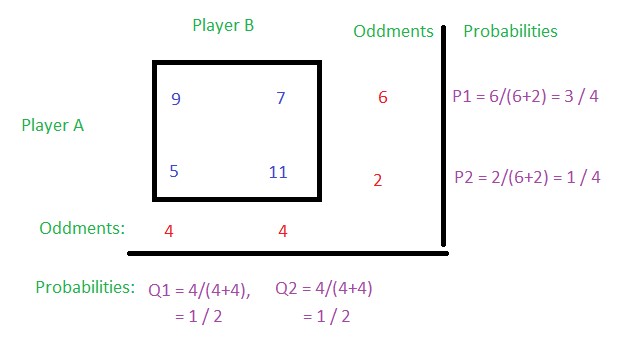
Calculating probabilities: Corresponding oddments/Sum of the row or column oddments, i.e.
For P1, oddment value of row 1 is 6 and the sum of oddment values of both rows is 8, so P1 = 6/(6+2) = 3/4
For P2, oddment value of row 2 is 2 and the sum of oddment values of both rows is 8, so P2 = 2/(6+2) = 1/4
For Q1, oddment value of column 1 is 4 and the sum of oddment values of both column is 8, so Q1 = 4/(4+4) = 1/2
For Q2, oddment value of column 2 is 4 and the sum of oddment values of both column is 8, so Q2 = 4/(4+4) = 1/2
-
Step 5: Find value of the game.
Using Formula

Without using Formula
There are 4 ways to find the value of the game.
Take the first column. Now multiply the elements of the first column with the corresponding row oddments, then add both multiplication and then divide it by the total oddments of row.
V = (9*6 + 5*2) / (6 + 2) = (54 + 10) / 8 = 64 / 8 = 8.
OR,
Take the second column. Now multiply the elements of the second column with the corresponding row oddments, then add both multiplication and then divide it by the total oddments of row.
V = (7*6 + 11*2) / (6+2) = (42 + 22) / 8 = 64 / 8 = 8.
OR,
Take the first row. Now multiply the elements of the first row with the corresponding column oddments, then add both multiplication and then divide it by the total oddments of column.
V = (9*4 + 7*4) / (4 + 4) = (36 + 28) / 8 = 64 / 8 = 8.
OR,
Take the second row. Now multiply the elements of the second row with the corresponding column oddments, then add both multiplication and then divide it by the total oddments of column.
V = (5*4 + 11*4) / (4 + 4) = (20 + 44) / 8 = 64 / 8 = 8.
-
Step 6: Hence, the strategies of Player A is (3/4, 1/4) and Player B is (1/2, 1/2), and the value of the game is V = 8. You can see that the probabilities of selection of each strategies for each player is less than 1 but the total probabilities for the respective player is 1. Total probabilities for player A is 3/4 + 1/4 = 1, and that of player B is 1/2 + 1/2 = 1.
Share your thoughts in the comments
Please Login to comment...