Puzzle | Game of Brussels Sprouts
Last Updated :
15 Feb, 2023
Given n number of spots, and two players. Players need to connect any two spots without intersecting any of the drawn line, the player who cannot give a move, loses. Determine who will win player1 or player2. Examples :
Input : n = 2
Output : player 2
Input : n = 3
Output : player 1
Explanation : 
Method : The winner of this game does not depend on the moves the players choose, rather it only depends on n. This problem can be solved using Euler Characteristics. According to Euler Characteristics : For every surface S there exists an integer 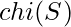 such that whenever a graph G with V vertices and E edges is embedded in S so that there are F faces(regions divided by the graph), then :
such that whenever a graph G with V vertices and E edges is embedded in S so that there are F faces(regions divided by the graph), then :
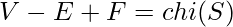
. For a planar graph
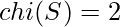
. Consider the final picture(i.e. situation after the last move).
 Solution Approach using Euler Characteristics:
Solution Approach using Euler Characteristics: 1. In the final picture we can take each cross point as a vertex. 2. Each line joining these cross points can be considered as an edge and 3. Each area section(including the outer one) can be considered as a face of the graph. Let, the number of moves possible for a particular n is m. To solve the problem, value of m must be found.
Observations : 1. There are initially n crosses(i.e. n vertices). Each move create one new cross. Hence, at last there will be total V = (n+m) crosses(vertices). 2. In each move as player join two free ends by a line and make a new cross in the line(creating a new vertex), next player end up with two new edges connecting the three vertices(old 2, new 1). Hence, after m moves there will be E = 2*m edges in the graph. 3. It can be seen that there is exactly one free end inside each of the faces. Hence, the number of faces is equal to total number of free ends. Again, in each move player connect two free ends(loss two free ends) and create two new free ends(by making one new cross point). Hence, the total number of free ends remains unchanged. So, total number of free ends initially = Number of faces, F = 4*n. Now, It can be written as : V – E + F = 2 i.e. (n + m) – 2*m + 4*n = 2. Solving this equation, m = (5*n – 2) Now if m is odd player 1 will win and if m is even player 2 will win.
C++
#include <iostream>
using namespace std;
void winner(int n)
{
int m = 5 * n - 2;
if (m % 2 == 1)
cout << "Player 1" << endl;
else
cout << "Player 2" << endl;
}
int main()
{
int n1 = 2;
winner(n1);
int n2 = 3;
winner(n2);
return 0;
}
|
Java
import java.io.*;
class GFG {
static void winner(int n)
{
int m = 5 * n - 2;
if (m % 2 == 1)
System.out.println("Player 1");
else
System.out.println("Player 2");
}
public static void main(String[] args)
{
int n1 = 2;
winner(n1);
int n2 = 3;
winner(n2);
}
}
|
Python3
def winner(n):
m = 5 * n - 2
if m % 2 == 1:
print("Player 1")
else:
print("Player 2")
n1 = 2
winner(n1)
n2 = 3
winner(n2)
|
C#
using System;
class GFG {
public static void winner(int n)
{
int m = 5 * n - 2;
if (m % 2 == 1)
Console.WriteLine("Player 1");
else
Console.WriteLine("Player 2");
}
static void Main() {
int n1 = 2;
winner(n1);
int n2 = 3;
winner(n2);
}
}
|
Javascript
function winner(n)
{
let m = 5 * n - 2;
if (m % 2 == 1)
console.log("Player 1");
else
console.log("Player 2");
}
let n1 = 2;
winner(n1);
let n2 = 3;
winner(n2);
|
Share your thoughts in the comments
Please Login to comment...