Find the type of triangle from the given sides
Last Updated :
01 Nov, 2023
Given three integers A, B, and C which denote the sides of a triangle, the task is to check that the triangle is a right-angled, acute-angled, or obtuse-angled triangle.
Examples:
Input: A = 1, B = 4, C = 3
Output: Obtuse-angled Triangle
Explanation:
Triangle with the sides 1, 2 and 3 is an obtuse-angled triangle
Input: A = 2, B = 2, C = 2
Output: Acute-angled Triangle
Explanation:
Triangle with the sides 2, 2, and 2 is an acute-angled triangle
Approach: The idea is to use the facts from the cosine law to check the type of triangle using these formulae –
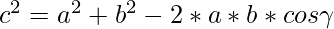
It generalizes the Pythagorean Theorem, which states that for a right-angled triangle square of the hypotenuse is equal to the sum of squares of the base and height of the triangle, which is 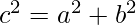
Similarly, It can be observed that
For acute-angled triangle
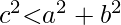
For Obtuse-angled triangle
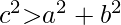
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void checkTypeOfTriangle(int a,
int b, int c){
int sqa = pow(a, 2);
int sqb = pow(b, 2);
int sqc = pow(c, 2);
if (sqa == sqb + sqc ||
sqb == sqc + sqa ||
sqc == sqa + sqb){
cout << "Right-angled Triangle";
}
else if(sqa > sqc + sqb ||
sqb > sqa + sqc ||
sqc > sqa + sqb){
cout << "Obtuse-angled Triangle";
}
else{
cout << "Acute-angled Triangle";
}
}
int main()
{
int a, b, c;
a = 2;
b = 2;
c = 2;
checkTypeOfTriangle(a, b, c);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void checkTypeOfTriangle(int a,
int b, int c){
int sqa = (int)Math.pow(a, 2);
int sqb = (int)Math.pow(b, 2);
int sqc = (int)Math.pow(c, 2);
if (sqa == sqa + sqb ||
sqb == sqa + sqc ||
sqc == sqa + sqb){
System.out.print("Right-angled Triangle");
}
else if(sqa > sqc + sqb ||
sqb > sqa + sqc ||
sqc > sqa + sqb){
System.out.print("Obtuse-angled Triangle");
}
else{
System.out.print( "Acute-angled Triangle");
}
}
public static void main (String []args)
{
int a, b, c;
a = 2;
b = 2;
c = 2;
checkTypeOfTriangle(a, b, c);
}
}
|
Python3
def checkTypeOfTriangle(a,b,c):
sqa = pow(a, 2)
sqb = pow(b, 2)
sqc = pow(c, 2)
if (sqa == sqc + sqb or
sqb == sqa + sqc or
sqc == sqa + sqb):
print("Right-angled Triangle")
elif(sqa > sqc + sqb or
sqb > sqa + sqc or
sqc > sqa + sqb):
print("Obtuse-angled Triangle")
else:
print("Acute-angled Triangle")
if __name__ == '__main__':
a = 2
b = 2
c = 2
checkTypeOfTriangle(a, b, c)
|
C#
using System;
class GFG
{
static void checkTypeOfTriangle(int a,
int b, int c){
int sqa = (int)Math.Pow(a, 2);
int sqb = (int)Math.Pow(b, 2);
int sqc = (int)Math.Pow(c, 2);
if (sqa == sqa + sqb ||
sqb == sqa + sqc ||
sqc == sqa + sqb){
Console.Write("Right-angled Triangle");
}
else if(sqa > sqc + sqb ||
sqb > sqa + sqc ||
sqc > sqa + sqb){
Console.Write("Obtuse-angled Triangle");
}
else{
Console.Write( "Acute-angled Triangle");
}
}
public static void Main(String []args)
{
int a, b, c;
a = 2;
b = 2;
c = 2;
checkTypeOfTriangle(a, b, c);
}
}
|
Javascript
<script>
function checkTypeOfTriangle(a,b,c)
{
let sqa = Math.floor(Math.pow(a, 2));
let sqb = Math.floor(Math.pow(b, 2));
let sqc = Math.floor(Math.pow(c, 2));
if (sqa == sqa + sqb ||
sqb == sqa + sqc ||
sqc == sqa + sqb){
document.write("Right-angled Triangle");
}
else if(sqa > sqc + sqb ||
sqb > sqa + sqc ||
sqc > sqa + sqb){
document.write("Obtuse-angled Triangle");
}
else{
document.write( "Acute-angled Triangle");
}
}
let a, b, c;
a = 2;
b = 2;
c = 2;
checkTypeOfTriangle(a, b, c);
</script>
|
OutputAcute-angled Triangle
Share your thoughts in the comments
Please Login to comment...