Find Sum of Series 1^2 – 2^2 + 3^2 – 4^2 ….. upto n terms
Last Updated :
25 Aug, 2022
Given a number n, the task is to find the sum of the below series upto n terms:
12 – 22 + 32 – 42 + …..
Examples:
Input: n = 2
Output: -3
Explanation:
sum = 12 - 22
= 1 - 4
= -3
Input: n = 3
Output: 6
Explanation:
sum = 12 - 22 + 32
= 1 - 4 + 9
= 6
Naive Approach:
This method involves simply running a loop of i from 1 to n and if i is odd then simply add its square to the result it i is even then simply subtract square of it to the result.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int sum_of_series(int n)
{
int result = 0;
for (int i = 1; i <= n; i++) {
if (i % 2 == 0)
result = result - pow(i, 2);
else
result = result + pow(i, 2);
}
return result;
}
int main(void)
{
int n = 3;
cout << sum_of_series(n) << endl;
n = 10;
cout << sum_of_series(n) << endl;
}
|
Java
import java.util.*;
import java.lang.*;
class GFG
{
static int sum_of_series(int n)
{
int result = 0;
for (int i = 1; i <= n; i++)
{
if (i % 2 == 0)
result = result -
(int)Math.pow(i, 2);
else
result = result +
(int)Math.pow(i, 2);
}
return result;
}
public static void main(String args[])
{
int n = 3;
System.out.println(sum_of_series(n));
n = 10;
System.out.println(sum_of_series(n));
}
}
|
Python3
def sum_of_series(n):
result = 0
for i in range(1, n + 1) :
if (i % 2 == 0):
result = result - pow(i, 2)
else:
result = result + pow(i, 2)
return result
if __name__ == "__main__":
n = 3
print(sum_of_series(n))
n = 10
print(sum_of_series(n))
|
C#
using System;
class GFG
{
static int sum_of_series(int n)
{
int result = 0;
for (int i = 1; i <= n; i++)
{
if (i % 2 == 0)
result = result -
(int)Math.Pow(i, 2);
else
result = result +
(int)Math.Pow(i, 2);
}
return result;
}
public static void Main()
{
int n = 3;
Console.WriteLine(sum_of_series(n));
n = 10;
Console.WriteLine(sum_of_series(n));
}
}
|
PHP
<?php
function sum_of_series($n)
{
$result = 0;
for ($i = 1; $i <= $n; $i++)
{
if ($i % 2 == 0)
$result = $result - pow($i, 2);
else
$result = $result + pow($i, 2);
}
return $result;
}
$n = 3;
echo sum_of_series($n),"\n";
$n = 10;
echo sum_of_series($n),"\n";
?>
|
Javascript
<script>
function sum_of_series(n)
{
var result = 0;
for (i = 1; i <= n; i++)
{
if (i % 2 == 0)
result = result -
parseInt(Math.pow(i, 2));
else
result = result +
parseInt(Math.pow(i, 2));
}
return result;
}
var n = 3;
document.write(sum_of_series(n)+ "<br>");
n = 10;
document.write(sum_of_series(n));
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Efficient Approach
It is based on condition of n
If n is even:
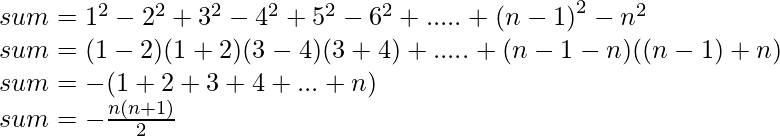
If n is odd:
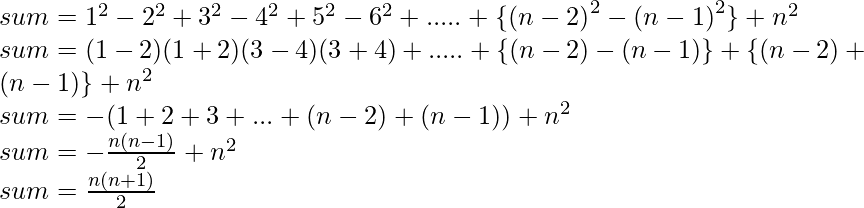
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int sum_of_series(int n)
{
int result = 0;
if (n % 2 == 0) {
result = -(n * (n + 1)) / 2;
}
else {
result = (n * (n + 1)) / 2;
}
return result;
}
int main(void)
{
int n = 3;
cout << sum_of_series(n) << endl;
n = 10;
cout << sum_of_series(n) << endl;
}
|
Java
import java.util.*;
import java.lang.*;
class GFG
{
static int sum_of_series(int n)
{
int result = 0;
if (n % 2 == 0)
{
result = -(n * (n + 1)) / 2;
}
else
{
result = (n * (n + 1)) / 2;
}
return result;
}
public static void main(String args[])
{
int n = 3;
System.out.println(sum_of_series(n));
n = 10;
System.out.println(sum_of_series(n));
}
}
|
Python3
def sum_of_series(n) :
result = 0
if (n % 2 == 0) :
result = -(n * (n + 1)) // 2
else :
result = (n * (n + 1)) // 2
return result
if __name__ == "__main__" :
n = 3
print(sum_of_series(n))
n = 10
print(sum_of_series(n))
|
C#
using System;
class GFG
{
static int sum_of_series(int n)
{
int result = 0;
if (n % 2 == 0)
{
result = -(n * (n + 1)) / 2;
}
else
{
result = (n * (n + 1)) / 2;
}
return result;
}
public static void Main()
{
int n = 3;
Console.WriteLine(sum_of_series(n));
n = 10;
Console.WriteLine(sum_of_series(n));
}
}
|
PHP
<?php
function sum_of_series($n)
{
$result = 0;
if ($n % 2 == 0)
{
$result = -($n * ($n + 1)) / 2;
}
else
{
$result = ($n * ($n + 1)) / 2;
}
return $result;
}
$n = 3;
echo sum_of_series($n);
echo ("\n");
$n = 10;
echo sum_of_series($n);
echo ("\n");
$n = 10;
?>
|
Javascript
<script>
function sum_of_series( n) {
let result = 0;
if (n % 2 == 0) {
result = -(n * (n + 1)) / 2;
}
else {
result = (n * (n + 1)) / 2;
}
return result;
}
let n = 3;
document.write(sum_of_series(n)+"<br/>");
n = 10;
document.write(sum_of_series(n));
</script>
|
Time Complexity: O(1), the code will run in a constant time.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...