Find the Nth term of the series 2 + 6 + 13 + 23 + . . .
Last Updated :
11 Aug, 2022
Given an integer N. The task is to write a program to find the Nth term of the given series:
2 + 6 + 13 + 23 + …
Examples:
Input : N = 5
Output : 36
Input : N = 10
Output : 146
Refer the article on How to find Nth term of series to know idea behind finding Nth term of any given series.
The generalized N-th term of given series is:
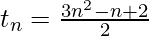
Below is the implementation of above approach:
C++
#include<bits/stdc++.h>
using namespace std;
int Nth_Term(int n)
{
return (3 * pow(n, 2) - n + 2) / (2);
}
int main()
{
int N = 5;
cout<<Nth_Term(N)<<endl;
}
|
Java
import java.io.*;
class GFG {
static int Nth_Term(int n)
{
return (int)(3 * Math.pow(n, 2) - n + 2) / (2);
}
public static void main (String[] args) {
int N = 5;
System.out.println(Nth_Term(N));
}
}
|
Python3
def Nth_Term(n):
return (3 * pow(n, 2) - n + 2) // (2)
N = 5
print(Nth_Term(N))
|
C#
class GFG
{
static int Nth_Term(int n)
{
return (int)(3 * System.Math.Pow(n, 2) -
n + 2) / (2);
}
static void Main ()
{
int N = 5;
System.Console.WriteLine(Nth_Term(N));
}
}
|
PHP
<?php
function Nth_Term($n)
{
return (3 * pow($n, 2) - $n + 2) / (2);
}
$N = 5;
echo (Nth_Term($N));
?>
|
Javascript
<script>
function Nth_Term(n)
{
return (3 * Math.pow(n, 2) - n + 2) / (2);
}
let N = 5;
document.write (Nth_Term(N));
</script>
|
Time complexity: O(1), since there is no loop or recursion.
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...