Sum of first N terms of Quadratic Sequence 3 + 7 + 13 + …
Last Updated :
20 Aug, 2022
Given a quadratic series as given below, the task is to find the sum of the first n terms of this series.
Sn = 3 + 7 + 13 + 21 + 31 + ….. + upto n terms
Examples:
Input: N = 3
Output: 23
Input: N = 4
Output: 44
Approach:
Let the series be represented as
Sn = 3 + 7 + 13 + ... + tn
where
- Sn represents the sum of the series till n terms.
- tn represents the nth term of the series.
Now, to formulate the series, the elements need to be formed by taking the difference of the consecutive elements of the series.
Equation 1: Sn = 3 + 7 + 13 + 21 + 31 +…..+ tn-1 + tn
Equation 2: Sn = 0 + 3 + 7 + 13 + 21 + 31 + …… + tn-1 + tn
(writing the above series by shifting all elements to right by 1 position)
Now, Subtract Equation 2 from Equation 1 i.e. (Equation 1 – Equation 2)
Sn – Sn = (3 – 0) + (7 – 3) + (13 – 7) + (31 – 21) + …… + (tn- tn-1) – tn
=> 0 = 3 + 4 + 6 + 8 + 10 + …… + (tn – tn-1) – tn
In the above series, leaving 3 aside, terms starting from 4 to (tn – tn-1) will form an A.P.
Since the formula of the sum of n terms of A.P. is:
Sn = n*(2*a + (n – 1)*d)/2
which implies,
In series: 4 + 6 + 8 + … + (tn – tn-1)
AP is formed with (n-1) terms.
Hence,
Sum of this series: (n-1)*(2*4 + (n-2)*2)/2
Therefore, the original series:
0 = 3 + (n-1)*(2*4 + (n-2)*2)/2 – tn
where tn = n^2 + n + 1 which is the nth term.
Therefore,
Sum of first n terms of series will be:
tn = n^2 + n + 1
Sn = 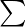 (n^2) +
(n^2) + 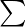 n +
n + 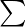 (1)
(1)
Sn = n*(n+1)*(n+2)/6 + n*(n+1)/2 + n
Sn = n*(n^2 + 3*n + 5)/3
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int calculateSum(int n)
{
return n * (pow(n, 2) + 3 * n + 5) / 3;
}
int main()
{
int n = 3;
cout << "Sum = " << calculateSum(n);
return 0;
}
|
Java
import java.util.*;
class solution
{
static int calculateSum(int n)
{
return n * (int) (Math.pow(n, 2) + 3 * n + 5 )/ 3;
}
public static void main(String arr[])
{
int n = 3;
System.out.println("Sum = " +calculateSum(n));
}
}
|
Python3
from math import pow
def calculateSum(n):
return n * (pow(n, 2) + 3 * n + 5) / 3
if __name__ == '__main__':
n = 3
print("Sum =", int(calculateSum(n)))
|
C#
using System;
class gfg
{
public double calculateSum(int n)
{
return (n * (Math.Pow(n, 2) + 3 * n + 5) / 3);
}
}
class geek
{
public static int Main()
{
gfg g = new gfg();
int n = 3;
Console.WriteLine( "Sum = {0}", g.calculateSum(n));
return 0;
}
}
|
PHP
<?php
function calculateSum($n)
{
return $n * (pow($n, 2) + 3 *
$n + 5) / 3;
}
$n = 3;
echo "Sum = " . calculateSum($n);
?>
|
Javascript
<script>
function calculateSum(n)
{
return n * (Math.pow(n, 2) + 3 * n + 5 ) / 3;
}
var n = 3;
document.write("Sum = " + calculateSum(n));
</script>
|
Time Complexity: O(1), since there is no loop or recursion.
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...