Find the maximum sum of Plus shape pattern in a 2-D array
Last Updated :
12 Sep, 2022
Given a 2-D array of size N*M where, 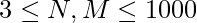 . The task is to find the maximum value achievable by a + shaped pattern. The elements of the array can be negative.
. The task is to find the maximum value achievable by a + shaped pattern. The elements of the array can be negative.
The plus(+) shape pattern is formed by taking any element with co-ordinate (x, y) as a center and then expanding it in all four directions(if possible).
A plus(+) shape has atleast five elements which are { (x-1, y), (x, y-1), (x, y), (x+1, y), (x, y+1) } i.e. the arms should have length>1 but not necessarily need to have same length.
Examples:
Input: N = 3, M = 4
1 1 1 1
-6 1 1 -4
1 1 1 1
Output: 0
Here, (x, y)=(2, 3) center of pattern(+).
Other four arms are, left arm = (2, 2), right arm = (2, 4),
up arm = (1, 3), down arm = (2, 3).
Hence sum of all elements are ( 1 + 1 + (-4) + 1 + 1 ) = 0.
Input: N = 5, M = 3
1 2 3
-6 1 -4
1 1 1
7 8 9
6 3 2
Output: 31
Approach: This problem is an application of the standard Largest Sum Contiguous Subarray.
We quickly pre-compute the maximum contiguous sub-sequence (subarray) sum for each row and column, in 4 directions, namely, Up, Down, Left and Right. This can be done using the standard Maximum contiguous sub-sequence sum of a 1-D array.
We make four 2-D array’s 1 for each direction.
- up[i][j]– Maximum sum contiguous sub-sequence of elements in upward direction, from rows 1, 2, 3, …, i More formally, it represents the maximum sum obtained by adding a contiguous sub-sequence of elements from list of arr[1][j], arr[2][j], …, arr[i][j]
- down[i][j] -Maximum sum contiguous sub-sequence of elements in downward direction, from rows i, i+1, i+2,,…, N More formally, it represents the maximum sum obtained by adding a contiguous sub-sequence of elements from list of arr[i][j], arr[i+1][j], …, arr[N][j]
- left[i][j]– Maximum sum contiguous sub-sequence of elements in left direction, from columns 1, 2, 3, …, j More formally, it represents the maximum sum obtained by adding a contiguous sub-sequence of elements from list of arr[i][1], arr[i][2], …, arr[i][j]
- right[i][j]– Maximum sum contiguous sub-sequence of elements in right direction, from columns j, j+1, j+2, …, M More formally, it represents the maximum sum obtained by adding a contiguous sub-sequence of elements from list of arr[i][j], arr[i][j+1], …, arr[i][M]
All that’s left is, to check each cell as a possible center of the + and use pre-computed data to find the value achieved by + shape in O(1).
![Rendered by QuickLaTeX.com Ans_{i, j} = up[i-1][j] + down[i+1][j] + left[i][j-1]+right[i][j+1]+arr[i][j]_{adding\;the\;value\;at \;center\; of\; +}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85b2556b416833463c94221bb5a0ccea_l3.png)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define N 100
const int n = 3, m = 4;
int maxPlus(int (&arr)[n][m])
{
int ans = INT_MIN;
int left[N][N], right[N][N], up[N][N], down[N][N];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
left[i][j] = max(0LL, (j ? left[i][j - 1] : 0LL))
+ arr[i][j];
up[i][j] = max(0LL, (i ? up[i - 1][j] : 0LL))
+ arr[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
right[i][j] = max(0LL, (j + 1 == m ? 0LL: right[i][j + 1]))
+ arr[i][j];
down[i][j] = max(0LL, (i + 1 == n ? 0LL: down[i + 1][j]))
+ arr[i][j];
}
}
for (int i = 1; i < n - 1; ++i)
for (int j = 1; j < m - 1; ++j)
ans = max(ans, up[i - 1][j] + down[i + 1][j]
+ left[i][j - 1] + right[i][j + 1] + arr[i][j]);
return ans;
}
int main()
{
int arr[n][m] = { { 1, 1, 1, 1 },
{ -6, 1, 1, -4 },
{ 1, 1, 1, 1 } };
cout << maxPlus(arr);
return 0;
}
|
Java
class GFG
{
public static int N = 100;
public static int n = 3, m = 4;
public static int maxPlus(int[][] arr)
{
int ans = Integer.MIN_VALUE;
int[][] left = new int[N][N];
int[][] right = new int[N][N];
int[][] up = new int[N][N];
int[][] down = new int[N][N];
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
left[i][j] = Math.max(0, ((j != 0) ? left[i][j - 1] : 0))
+ arr[i][j];
up[i][j] = Math.max(0, ((i != 0)? up[i - 1][j] : 0))
+ arr[i][j];
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
right[i][j] = Math.max(0, (j + 1 == m ? 0: right[i][j + 1]))
+ arr[i][j];
down[i][j] = Math.max(0, (i + 1 == n ? 0: down[i + 1][j]))
+ arr[i][j];
}
}
for (int i = 1; i < n - 1; ++i)
for (int j = 1; j < m - 1; ++j)
ans = Math.max(ans, up[i - 1][j] + down[i + 1][j]
+ left[i][j - 1] + right[i][j + 1] + arr[i][j]);
return ans;
}
public static void main(String[] args) {
int[][] arr = new int[][]{ { 1, 1, 1, 1 },
{ -6, 1, 1, -4 },
{ 1, 1, 1, 1 } };
System.out.println( maxPlus(arr) );
}
}
|
Python 3
N = 100
n = 3
m = 4
def maxPlus(arr):
ans = 0
left = [[0 for x in range(N)]
for y in range(N)]
right = [[0 for x in range(N)]
for y in range(N)]
up = [[0 for x in range(N)]
for y in range(N)]
down = [[0 for x in range(N)]
for y in range(N)]
for i in range(n) :
for j in range(m) :
left[i][j] = (max(0, (left[i][j - 1] if j else 0)) +
arr[i][j])
up[i][j] = (max(0, (up[i - 1][j] if i else 0)) +
arr[i][j])
for i in range(n) :
for j in range(m) :
right[i][j] = max(0, (0 if (j + 1 == m ) else
right[i][j + 1])) + arr[i][j]
down[i][j] = max(0, (0 if (i + 1 == n ) else
down[i + 1][j])) + arr[i][j]
for i in range(1, n - 1):
for j in range(1, m - 1):
ans = max(ans, up[i - 1][j] + down[i + 1][j] +
left[i][j - 1] + right[i][j + 1] +
arr[i][j])
return ans
if __name__ == "__main__":
arr = [[ 1, 1, 1, 1 ],
[ -6, 1, 1, -4 ],
[ 1, 1, 1, 1 ]]
print(maxPlus(arr))
|
C#
using System;
class GFG
{
public static int N = 100;
public static int n = 3, m = 4;
public static int maxPlus(int[,] arr)
{
int ans = int.MinValue;
int[,] left = new int[N,N];
int[,] right = new int[N,N];
int[,] up = new int[N,N];
int[,] down = new int[N,N];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
left[i,j] = Math.Max(0, ((j != 0) ? left[i,j - 1] : 0))
+ arr[i,j];
up[i,j] = Math.Max(0, ((i != 0)? up[i - 1,j] : 0))
+ arr[i,j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
right[i,j] = Math.Max(0, (j + 1 == m ? 0: right[i,j + 1]))
+ arr[i,j];
down[i,j] = Math.Max(0, (i + 1 == n ? 0: down[i + 1,j]))
+ arr[i,j];
}
}
for (int i = 1; i < n - 1; ++i)
for (int j = 1; j < m - 1; ++j)
ans = Math.Max(ans, up[i - 1,j] + down[i + 1,j]
+ left[i,j - 1] + right[i,j + 1] + arr[i,j]);
return ans;
}
static void Main()
{
int[,] arr = new int[,]{ { 1, 1, 1, 1 },
{ -6, 1, 1, -4 },
{ 1, 1, 1, 1 } };
Console.Write( maxPlus(arr) );
}
}
|
Javascript
<script>
let N = 100;
let n = 3, m = 4;
function maxPlus(arr)
{
let ans = 0;
let left = new Array(N);
let right = new Array(N);
let up = new Array(N);
let down = new Array(N);
for(let i=0;i<N;i++)
{
left[i]=new Array(N);
right[i]=new Array(N);
up[i]=new Array(N);
down[i]=new Array(N);
for(let j=0;j<N;j++)
{
left[i][j]=0;
right[i][j]=0;
up[i][j]=0;
down[i][j]=0;
}
}
for (let i = 0; i < n; i++)
{
for (let j = 0; j < m; j++)
{
left[i][j] = Math.max(0, ((j != 0) ?
left[i][j - 1] : 0))
+ arr[i][j];
up[i][j] = Math.max(0, ((i != 0)?
up[i - 1][j] : 0))
+ arr[i][j];
}
}
for (let i = 0; i < n; i++)
{
for (let j = 0; j < m; j++)
{
right[i][j] = Math.max(0, (j + 1 == m ?
0: right[i][j + 1])) + arr[i][j];
down[i][j] = Math.max(0, (i + 1 == n ? 0:
down[i + 1][j])) + arr[i][j];
}
}
for (let i = 1; i < n - 1; ++i)
for (let j = 1; j < m - 1; ++j)
{
ans = Math.max(ans, up[i - 1][j] +
down[i + 1][j] + left[i][j - 1] +
right[i][j + 1] + arr[i][j]);
}
return ans;
}
let arr = [[ 1, 1, 1, 1 ],
[ -6, 1, 1, -4 ],
[ 1, 1, 1, 1 ]];
document.write(maxPlus(arr));
</script>
|
Time Complexity: O(N*M) for given N rows and M columns
Auxiliary Space: O(N*M)
Share your thoughts in the comments
Please Login to comment...