Find the length of the median of a Triangle if length of sides are given
Last Updated :
06 Jan, 2024
Given the length of all three sides of a triangle as a, b and c. The task is to calculate the length of the median of the triangle.
A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side.
Examples:
Input: a = 8, b = 10, c = 13
Output: 10.89
Input: a = 4, b = 3, c = 5
Output: 3.61
Approach: The idea is to use Apollonius’s theorem to solve this problem.
Apollonius’s Theorem states that “the sum of the squares of any two sides of a triangle equals twice the square on half the third side and twice the square on the median bisecting the third side”.
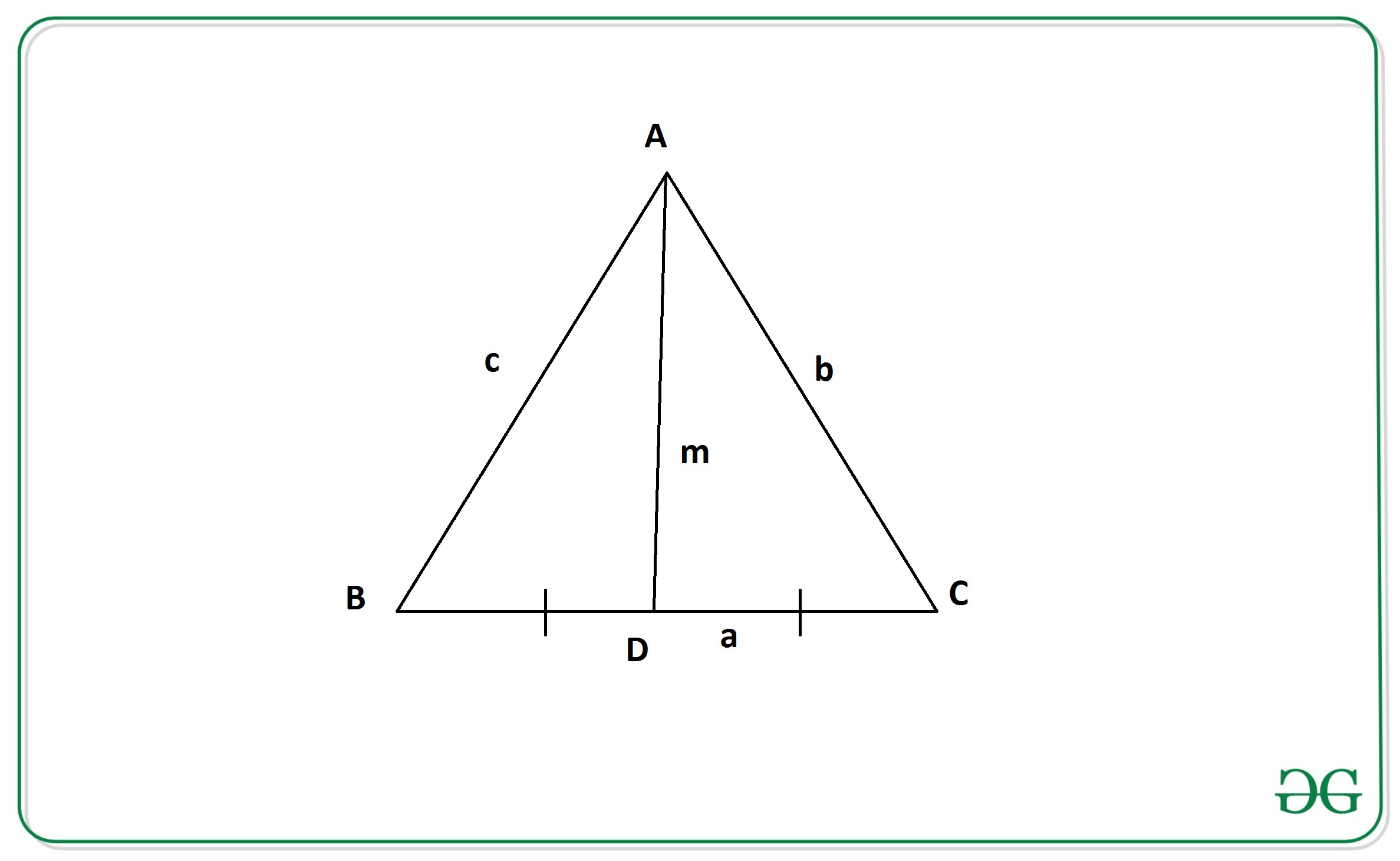
From the above figure, According to Apollonius’s Theorem we have:

where a, b, and c are the length of sides of the triangle
and m is the length of median of the triangle on side 2*a
Therefore, the length of the median of a triangle from the above equation is given by:

Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
float median(int a, int b, int c)
{
float n = sqrt(2 * b * b +
2 * c * c - a * a) / 2;
return n;
}
int main()
{
int a, b, c;
a = 4;
b = 3;
c = 5;
float ans = median(a, b, c);
cout << fixed << setprecision(2) << ans;
return 0;
}
|
Java
import java.util.*;
class GFG{
public static float median(int a, int b, int c)
{
float n = (float)(Math.sqrt(2 * b * b +
2 * c * c -
a * a) / 2);
return n;
}
public static void main(String[] args)
{
int a, b, c;
a = 4;
b = 3;
c = 5;
float ans = median(a, b, c);
System.out.println(String.format("%.2f", ans));
}
}
|
Python3
import math
def median(a, b, c):
n = (1 / 2)*math.sqrt(2*(b**2)
+ 2*(c**2)
- a**2)
return n
a = 4
b = 3
c = 5
ans = median(a, b, c)
print(round(ans, 2))
|
C#
using System;
class GFG{
public static float median(int a, int b, int c)
{
float n = (float)(Math.Sqrt(2 * b * b +
2 * c * c -
a * a) / 2);
return n;
}
public static void Main(String[] args)
{
int a, b, c;
a = 4;
b = 3;
c = 5;
float ans = median(a, b, c);
Console.WriteLine(String.Format("{0:F2}", ans));
}
}
|
Javascript
<script>
function median(a, b, c)
{
let n = (Math.sqrt(2 * b * b +
2 * c * c -
a * a) / 2);
return n;
}
let a, b, c;
a = 4;
b = 3;
c = 5;
let ans = median(a, b, c);
document.write(ans, 2);
</script>
|
Time Complexity: O(log(n)) because using inbuilt sqrt function
Space Complexity: O(1)
Share your thoughts in the comments
Please Login to comment...