Find minimum speed to finish all Jobs
Last Updated :
17 Apr, 2023
Given an array A and an integer H where ![Rendered by QuickLaTeX.com 1\leq A[i] \leq 10^{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa25f6a1c7dc06a2f1b9930da2eefcce_l3.png) and
and 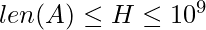 . Each element A[i] represents remaining pending jobs to be done and H represents hours left to complete all of the jobs. The task is to find the minimum speed in jobs per Hour at which person needs to work to complete all jobs in H hours.
. Each element A[i] represents remaining pending jobs to be done and H represents hours left to complete all of the jobs. The task is to find the minimum speed in jobs per Hour at which person needs to work to complete all jobs in H hours.
Note: If A[i] has less job to be done than speed of person then he finish all of the work of A[i] and won’t go to next element during this hour.
Examples:
Input: A[] = [3, 6, 7, 11], H = 8
Output: 4
Input: A[] = [30, 11, 23, 4, 20], H = 5
Output: 30
Approach: If the person can finish all the jobs (within H hours) with an speed of K jobs/hour then he can finish all jobs with a larger speed too.
If we let ispossible(K) be true if and only if the person can finish with a job speed of K, then there is some X such that ispossible(K) = True if and only if K >= X.
For example, with A = [3, 6, 7, 11] and H = 8, there is some X = 4 so that ispossible(1) = ispossible(2) = ispossible(3) = False, and ispossible(4) = ispossible(5) = … = True.
We can do a binary search on the values of ispossible(K) to find the first X such that ispossible(X) is True which will be our answer.
Now, as it is not allowed to move from one element to other during the current hour even if the job is completed than the maximum possible value of K can be the maximum element in the array A[]. So, to find the value of ispossible(K), (i.e. whether person with a job speed of K can finish all jobs in H hours), do binary search in the range (1, max_element_of_array).
Also, for each A[i] of jobs > 0, we can deduce that person finishes it in Math.ceil(A[i] / K) or ((A[i]-1) / K) + 1 hours, and we add these for all elements to find the total time to complete all of the jobs and compare it with H to check if it is possible to finish all jobs with a speed of K jobs/hour.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPossible(int A[], int n, int H, int K)
{
int time = 0;
for (int i = 0; i < n; ++i)
time += (A[i] - 1) / K + 1;
return time <= H;
}
int minJobSpeed(int A[], int n, int H)
{
if (H < n)
return -1;
int* max = max_element(A, A + n);
int lo = 1, hi = *max;
while (lo < hi) {
int mi = lo + (hi - lo) / 2;
if (!isPossible(A, n, H, mi))
lo = mi + 1;
else
hi = mi;
}
return lo;
}
int main()
{
int A[] = { 3, 6, 7, 11 }, H = 8;
int n = sizeof(A) / sizeof(A[0]);
cout << minJobSpeed(A, n, H);
return 0;
}
|
Java
class GFG
{
static int findmax(int[] A)
{
int r = A[0];
for(int i = 1; i < A.length; i++)
r = Math.max(r, A[i]);
return r;
}
static boolean isPossible(int[] A, int n,
int H, int K)
{
int time = 0;
for (int i = 0; i < n; ++i)
time += (A[i] - 1) / K + 1;
return time <= H;
}
static int minJobSpeed(int[] A,
int n, int H)
{
if (H < n)
return -1;
int max = findmax(A);
int lo = 1, hi = max;
while (lo < hi)
{
int mi = lo + (hi - lo) / 2;
if (!isPossible(A, n, H, mi))
lo = mi + 1;
else
hi = mi;
}
return lo;
}
public static void main(String[] args)
{
int[] A = { 3, 6, 7, 11 };
int H = 8;
int n = A.length;
System.out.println(minJobSpeed(A, n, H));
}
}
|
C#
using System;
using System.Linq;
class GFG{
static bool isPossible(int[] A, int n, int H, int K)
{
int time = 0;
for (int i = 0; i < n; ++i)
time += (A[i] - 1) / K + 1;
return time <= H;
}
static int minJobSpeed(int[] A, int n, int H)
{
if (H < n)
return -1;
int max = A.Max();
int lo = 1, hi = max;
while (lo < hi) {
int mi = lo + (hi - lo) / 2;
if (!isPossible(A, n, H, mi))
lo = mi + 1;
else
hi = mi;
}
return lo;
}
public static void Main()
{
int[] A = { 3, 6, 7, 11 };
int H = 8;
int n = A.Length;
Console.WriteLine(minJobSpeed(A, n, H));
}
}
|
Python3
def isPossible(A, n, H, K):
time = 0
for i in range(n):
time += (A[i] - 1) // K + 1
return time <= H
def minJobSpeed(A, n, H):
if H < n:
return -1
Max = max(A)
lo, hi = 1, Max
while lo < hi:
mi = lo + (hi - lo) // 2
if not isPossible(A, n, H, mi):
lo = mi + 1
else:
hi = mi
return lo
if __name__ == "__main__":
A = [3, 6, 7, 11]
H = 8
n = len(A)
print(minJobSpeed(A, n, H))
|
Javascript
<script>
function isPossible(A, n, H, K)
{
var time = 0;
for (var i = 0; i < n; ++i)
time += parseInt((A[i] - 1) / K) + 1;
return time <= H;
}
function minJobSpeed(A, n, H)
{
if (H < n)
return -1;
var max = A.reduce((a,b)=> Math.max(a,b));
var lo = 1, hi = max;
while (lo < hi) {
var mi = lo + parseInt((hi - lo) / 2);
if (!isPossible(A, n, H, mi))
lo = mi + 1;
else
hi = mi;
}
return lo;
}
var A = [3, 6, 7, 11], H = 8;
var n = A.length;
document.write( minJobSpeed(A, n, H));
</script>
|
Complexity analysis:
The time complexity of this program is O(N log M), where N is the length of the input array A and M is the maximum element in A. This is because the binary search is performed on the range [1, M], and for each mid-point, the isPossible function is called, which has a time complexity of O(N).
The space complexity of the program is O(1), as only a constant amount of memory is used to store variables that do not depend on the size of the input. The input array A is not modified during the execution of the program, so it does not contribute to the space complexity.
Share your thoughts in the comments
Please Login to comment...