Find minimum area of rectangle with given set of coordinates

Given an array 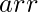arr of set of points in the X-Y plane. The task is to find the minimum area of a rectangle that can be formed from these points. The sides of the rectangle should be parallel to the X and Y axes. If a rectangle cannot be formed with the given points then print 0.

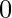Examples:

Input: arr[][] = [[1, 1], [1, 3], [3, 1], [3, 3], [2, 2]]
Output: 4
The only rectangle possible will be formed with the points (1, 1), (1, 3), (3, 1) and (3, 3)



Input: arr[][] = [[1, 1], [1, 3], [3, 1], [3, 3], [4, 1], [4, 3]]
Output: 2

Approach: Group the points by 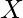X coordinates, so that points on straight vertical lines are grouped together. Then, for every pair of points in a group, for eg. coordinates (X, Y1) and (X, Y2), we check for the smallest rectangle with this pair of points as the rightmost edge of the rectangle to be formed. We can do this by keeping track of all other pairs of points we’ve visited before. Finally return the minimum possible area of the rectangle obtained.

Below is the implementation of the above approach:

CPP

filter_none

edit
close

play_arrow

link
brightness_4
code

// C++ Implementation of above approach
#include <bits/stdc++.h>
using namespace std;
  
// function to find minimum area of Rectangle
int minAreaRect(vector<vector<int>> A){
  
    // creating empty columns
    map<int,vector<int>> columns;
  
    // fill columns with coordinates
    for(auto i:A)
        columns[i[0]].push_back(i[1]);
  
    map<pair<int,int>,int > lastx;
  
    int ans = INT_MAX;
  
    for (auto x:columns)
    {
        vector<int> column = x.second;
        sort(column.begin(), column.end());
        for (int j = 0; j < column.size(); j++)
        {
            for (int i = 0; i < j; i++)
            {
                int y1 = column[i];
  
                // check if rectangle can be formed
                if (lastx.find({y1, column[j]}) != lastx.end())
                {
                    ans = min(ans, (x.first - lastx[{y1, column[j]}]) *
                            (column[j] - column[i]));
                }
                lastx[{y1, column[j]}] = x.first;
            }
            }
        }
  
    if (ans < INT_MAX)
        return ans;
    else
        return 0;
}
  
// Driver code
int main()
{
    vector<vector<int>> A = {{1, 1}, {1, 3}, {3, 1}, {3, 3}, {2, 2}};
    cout << (minAreaRect(A));
    return 0;
}
  
// This code is contributed by mohit kumar 29

chevron_right






                        filter_none









Python














                                    filter_none




                                    edit

                                    close




                                    play_arrow




                                    link

                                    brightness_4

                                    code
                                




















# Python Implementation of above approach 


import collections 


  


# function to find minimum area of Rectangle 


def minAreaRect(A): 


  


    # creating empty columns 


    columns = collections.defaultdict(list) 


  


    # fill columns with coordinates 


    for x, y in A: 


        columns[x].append(y) 


  


    lastx = {} 


    ans = float('inf') 


  


    for x in sorted(columns): 


        column = columns[x] 


        column.sort() 


        for j, y2 in enumerate(column): 


            for i in range(j): 


                y1 = column[i] 


  


                # check if rectangle can be formed 


                if (y1, y2) in lastx: 


                    ans = min(ans, (x - lastx[y1, y2]) * (y2 - y1)) 


                lastx[y1, y2] = x 


  


    if ans < float('inf'): 


        return ans 


    else: 


        return 0


  


# Driver code 


A = [[1, 1], [1, 3], [3, 1], [3, 3], [2, 2]] 


print(minAreaRect(A)) 



















                        chevron_right







                        filter_none











Output:


4








    

        My Personal Notes
        arrow_drop_up
    

    

        
        

            
            
        

    


Recommended Posts:
Sanjit_Prasad
Check out this Author's contributed articles.
If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please Improve this article if you find anything incorrect by clicking on  the "Improve Article" button below.


Improved By :  mohit kumar 29