Find Kth smallest value for b such that a + b = a | b
Last Updated :
20 Feb, 2022
Given the numbers a and k, the task is to find the k’th smallest value for b such that a + b = a | b, where ‘|’ denotes the bitwise OR operator. The maximum value of a and k can be 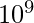 .
.
Examples:
Input: a = 10, k = 3
Output: 5
Numbers satisfying the condition 5 + b = 5 | b
are 1, 4, 5, etc.
Since 3rd smallest value for b is required,
hence b = 5.
Input: a = 1, k = 1
Output: 2
Numbers satisfying the condition 1 + b = 1 | b
are 2, 4, 6, etc.
Since 1st smallest value for b is required,
hence b = 2.
Approach:
- b is a solution of the given equation if and only if b has 0 in all positions where a has 1 (in binary notation).
- So, we need to determine the bit of b for positions where a has 0. Let, if a = 10100001 then the last eight digits of b must be b = 0*0****0, where ‘*’ denotes either 0 or 1. Any replacement of all ‘*’ by 0 or 1 gives us a solution.
- The k-th smallest number will be received by replacing all ‘*’ in y by digits of the binary representation of the number k.
- As the maximum value of a and k is
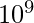 , so checking up to 32 positions in binary representation is enough to get the correct answer for the given equation.
, so checking up to 32 positions in binary representation is enough to get the correct answer for the given equation.
Below is the implementation of the above approach:
CPP
#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll kthSmallest(ll a, ll k)
{
ll res = 0;
ll j = 0;
for (ll i = 0; i < 32; i++) {
while (j < 32 && (a & (1 << j)))
j++;
if (k & (1 << i))
res |= (1LL << j);
j++;
}
return res;
}
int main()
{
ll a = 10, k = 3;
cout << kthSmallest(a, k) << "\n";
return 0;
}
|
Java
class GFG
{
static int kthSmallest(int a, int k)
{
int res = 0;
int j = 0;
for (int i = 0; i < 32; i++)
{
while (j < 32 && (a & (1 << j)) > 0)
j++;
if ((k & (1 << i)) > 0)
res |= (1 << j);
j++;
}
return res;
}
public static void main(String[] args)
{
int a = 10, k = 3;
System.out.print(kthSmallest(a, k) + "\n");
}
}
|
Python
def kthSmallest(a, k):
res = 0
j = 0
for i in range(32):
while (j < 32 and (a & (1 << j))):
j += 1
if (k & (1 << i)):
res |= (1 << j)
j += 1
return res
a = 10
k = 3
print(kthSmallest(a, k))
|
C#
using System;
class GFG
{
static int kthSmallest(int a, int k)
{
int res = 0;
int j = 0;
for (int i = 0; i < 32; i++)
{
while (j < 32 && (a & (1 << j)) > 0)
j++;
if ((k & (1 << i)) > 0)
res |= (1 << j);
j++;
}
return res;
}
public static void Main()
{
int a = 10, k = 3;
Console.WriteLine(kthSmallest(a, k));
}
}
|
Javascript
<script>
function kthSmallest(a, k)
{
var res = 0;
var j = 0;
for (var i = 0; i < 32; i++) {
while (j < 32 && (a & (1 << j)))
j++;
if (k & (1 << i))
res |= (1 << j);
j++;
}
return res;
}
var a = 10, k = 3;
document.write( kthSmallest(a, k));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...