Find if there is a path between two vertices in a directed graph | Set 2
Last Updated :
30 Jun, 2021
Given a Directed Graph and two vertices in it, check whether there is a path from the first given vertex to second.
Example:
Consider the following Graph:
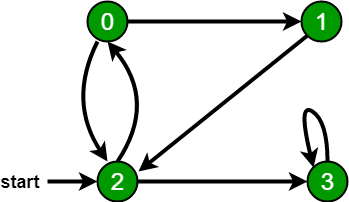
Input : (u, v) = (1, 3)
Output: Yes
Explanation:
There is a path from 1 to 3, 1 -> 2 -> 3
Input : (u, v) = (3, 6)
Output: No
Explanation:
There is no path from 3 to 6
A BFS or DFS based solution of this problem is discussed here.
Approach: Here we will discuss a Dynamic Programming based solution using Floyd Warshall Algorithm.
- Create a boolean 2D matrix mat where mat[i][j] will be true if there is a path from vertex i to j.
- For every starting vertex i and ending vertex j iterate over all intermediate vertex k and do check if there is a path for i to j through k then mark mat[i][j] as true.
- Finally, check if mat[u][v] is true then return true else return false.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define X 6
#define Z 2
bool existPath(int V, int edges[X][Z],
int u, int v)
{
bool mat[V][V];
memset(mat, false, sizeof(mat));
for (int i = 0; i < X; i++)
mat[edges[i][0]][edges[i][1]] = true;
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
mat[i][j] = mat[i][j]
|| mat[i][k]
&& mat[k][j];
}
}
}
if (u >= V || v >= V) {
return false;
}
if (mat[u][v])
return true;
return false;
}
int main()
{
int V = 4;
int edges[X][Z]
= { { 0, 2 }, { 0, 1 },
{ 1, 2 }, { 2, 3 },
{ 2, 0 }, { 3, 3 } };
int u = 1, v = 3;
if (existPath(V, edges, u, v))
cout << "Yes\n";
else
cout << "No\n";
return 0;
}
|
Java
import java.util.*;
class GFG{
static final int X = 6;
static final int Z = 2;
static boolean existPath(int V, int edges[][],
int u, int v)
{
boolean [][]mat = new boolean[V][V];
for (int i = 0; i < X; i++)
mat[edges[i][0]][edges[i][1]] = true;
for(int k = 0; k < V; k++)
{
for(int i = 0; i < V; i++)
{
for(int j = 0; j < V; j++)
{
mat[i][j] = mat[i][j] ||
mat[i][k] &&
mat[k][j];
}
}
}
if (u >= V || v >= V)
{
return false;
}
if (mat[u][v])
return true;
return false;
}
public static void main(String[] args)
{
int V = 4;
int edges[][] = { { 0, 2 }, { 0, 1 },
{ 1, 2 }, { 2, 3 },
{ 2, 0 }, { 3, 3 } };
int u = 1, v = 3;
if (existPath(V, edges, u, v))
System.out.print("Yes\n");
else
System.out.print("No\n");
}
}
|
Python3
X = 6
Z = 2
def existPath(V, edges, u, v):
mat = [[False for i in range(V)]
for j in range(V)]
for i in range(X):
mat[edges[i][0]][edges[i][1]] = True
for k in range(V):
for i in range(V):
for j in range(V):
mat[i][j] = (mat[i][j] or
mat[i][k] and
mat[k][j])
if (u >= V or v >= V):
return False
if (mat[u][v]):
return True
return False
V = 4
edges = [ [ 0, 2 ], [ 0, 1 ],
[ 1, 2 ], [ 2, 3 ],
[ 2, 0 ], [ 3, 3 ] ]
u, v = 1, 3
if (existPath(V, edges, u, v)):
print("Yes")
else:
print("No")
|
C#
using System;
class GFG{
static readonly int X = 6;
static readonly int Z = 2;
static bool existPath(int V, int [,]edges,
int u, int v)
{
bool [,]mat = new bool[V, V];
for (int i = 0; i < X; i++)
mat[edges[i, 0], edges[i, 1]] = true;
for(int k = 0; k < V; k++)
{
for(int i = 0; i < V; i++)
{
for(int j = 0; j < V; j++)
{
mat[i, j] = mat[i, j] ||
mat[i, k] &&
mat[k, j];
}
}
}
if (u >= V || v >= V)
{
return false;
}
if (mat[u, v])
return true;
return false;
}
public static void Main(String[] args)
{
int V = 4;
int [,]edges = { { 0, 2 }, { 0, 1 },
{ 1, 2 }, { 2, 3 },
{ 2, 0 }, { 3, 3 } };
int u = 1, v = 3;
if (existPath(V, edges, u, v))
Console.Write("Yes\n");
else
Console.Write("No\n");
}
}
|
Javascript
<script>
var X = 6;
var Z = 2;
function existPath(V, edges, u, v)
{
var mat = Array.from(Array(V), ()=>Array(V));
for (var i = 0; i < X; i++)
mat[edges[i][0]][edges[i][1]] = true;
for(var k = 0; k < V; k++)
{
for(var i = 0; i < V; i++)
{
for(var j = 0; j < V; j++)
{
mat[i][j] = mat[i][j] ||
mat[i][k] &&
mat[k][j];
}
}
}
if (u >= V || v >= V)
{
return false;
}
if (mat[u][v])
return true;
return false;
}
var V = 4;
var edges = [ [ 0, 2 ], [ 0, 1 ],
[ 1, 2 ], [ 2, 3 ],
[ 2, 0 ], [ 3, 3 ] ];
var u = 1, v = 3;
if (existPath(V, edges, u, v))
document.write("Yes<br>");
else
document.write("No<br>");
</script>
|
Time Complexity : O ( V 3)
Auxiliary Space : O ( V 2)
Share your thoughts in the comments
Please Login to comment...