Even and Odd Permutations and their theorems
Last Updated :
12 Jul, 2022
Even Permutations:
A permutation is called even if it can be expressed as a product of even number of transpositions.
Example-1:

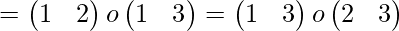
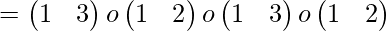
Here we can see that the permutation ( 1 2 3 ) has been expressed as a product of transpositions in three ways and in each of them the number of transpositions is even, so it is an even permutation.
Example-2:
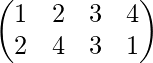
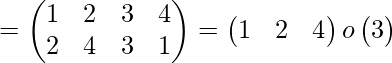

The given permutation is the product of two transpositions so it is an even permutation.
Odd Permutations:
A permutation is called odd if it can be expressed as a product of odd number of transpositions.
Example-1:
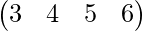
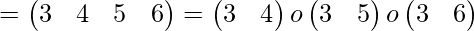
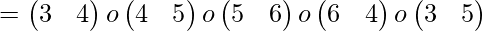
Here we can see that the permutation ( 3 4 5 6 ) has been expressed as a product of transpositions in two ways and in each of them number of transpositions is odd, so it is an odd permutation.
Example-2:
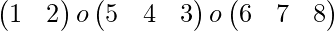
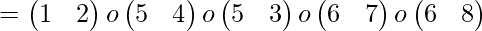
The given permutation is the product of five transposes so it is an odd permutation.
Theorems on Even and Odd Permutations :
Theorem-1:
If P1 and P2 are permutations, then
- (a) P1 P2 is even provided P1 and P2 are either both even or both odd.
- (b) P1 P2 is odd provided one of P1 and P2 is odd and the other even.
Proof: (a)
Case I. If P1, P2 both are even.
Let P1 and P2 be the product of 2n and 2m transpositions respectively, where n and m are positive integers.
Then each of P1 P2 and P2 P1 is product of 2n + 2m transpositions, where 2n + 2m is evidently an even integer.
Hence, P1 P2 and P2 P1 are even permutations.
Case II. If P1, P2 , both are odd. Let P1 P2 be the product of (2n + 1) and (2m + 1) transpositions respectively, where n and m are positive integers.
Then each of P1 P2 and P2 P1 is the product (2n + 1) + (2m + 1) i.e., 2 (n + m + 1) transpositions, where 2(n + m + 1) is evidently an even integer.
Hence, P1 P2 and P2 P1 are even permutations.
Proof : (b)
Let P1 be an odd and P2 be an even permutation. Also let P1 and P2 be the product of (2n + 1) and 2m transpositions respectively, where n and m are positive integers.
Then each of P1 P2 and P2 P1 is the product of (2n + 1) + 2m i.e. [ 2 ( n+ m )+1] transpositions , where 2(n+ m) + 1 is evidently an odd integer.
Hence P1 P2 and P2 P1 are odd permutations.
Theorem-2:
The Identity permutation is an even permutation.
Proof-: The identity permutation l can always be expressed as the product of two (i.e., even) transpositions.
For example
Hence I is an even permutation. (See definition)
Theorem-3:
The inverse of an even permutation is an even permutation.
Proof-: If P be an even permutation and P-1 be its inverse, then PP-1= I, the identity permutation.
But P and I are even (See Theorem 2 above),
so P-1 is also even (See Theorem 1 (a) above)
Theorem-4:
The inverse of an odd permutation is an odd permutation.
Proof-: If P be an odd permutation and P-1 be its inverse, then PP-1= I, the identity permutation.
But P is odd and I is even. (See Theorem 2 above),
so P-1 is also odd. (See Theorem 1 (b) above)
Share your thoughts in the comments
Please Login to comment...