Even and Odd Functions

Even and odd functions are types of functions. A function f is even if f(-x) = f(x), for all x in the domain of f. A function f is an odd function if f(-x) = -f(x) for all x in the domain of f, i.e.

• Even function: f(-x) = f(x)
• Odd function: f(-x) = -f(x)

In this article, we will discuss even and odd functions, even and odd function definitions, even and odd functions in trigonometry, and even and odd function graphs and others in detail.

What are Even and Odd Functions?

In mathematics, there are various kinds of functions that we examine. We can use algebra or graphics to determine whether a function is even or odd. Whereas, if a function f(x) meets the following condition for every x in its domain:

f(x) = f(-x), then it is considered even

On the other side, if a function f(x) meets the following condition for every x in its domain:

f(x) = -f(-x), then it is considered odd

Even and Odd Functions Definition

A real-valued function is regarded as even or odd that is symmetrical. Plugging (-x) in place of x in the function f(x) allows us to detect if a function is even or odd. Therefore, we may determine the type of function by looking at the output value of f(-x).

So, let’s see the following definitions that are given below:

Even Function

When all values of x and −x in the domain of f satisfy the following equation, the function “f” is considered even:

f(x) = f(-x)

Here, “Even” is symmetric about the y-axis indicating the graphical Function that would stay unmodified if you were to represent it across the y-axis.

Even Function Examples

Examples of even functions includes:

• cos x
• x², x⁴, x⁶, x⁸,…, i.e. xⁿ is an even function when n is an even integer
• |x|
• cos²x
• sin²x

Even Functions Graph

An even function’s graph is symmetric about the y-axis and stays unchanged after reflection of the y-axis. Along the whole curve, the function value will not change for any two opposing input values of x.

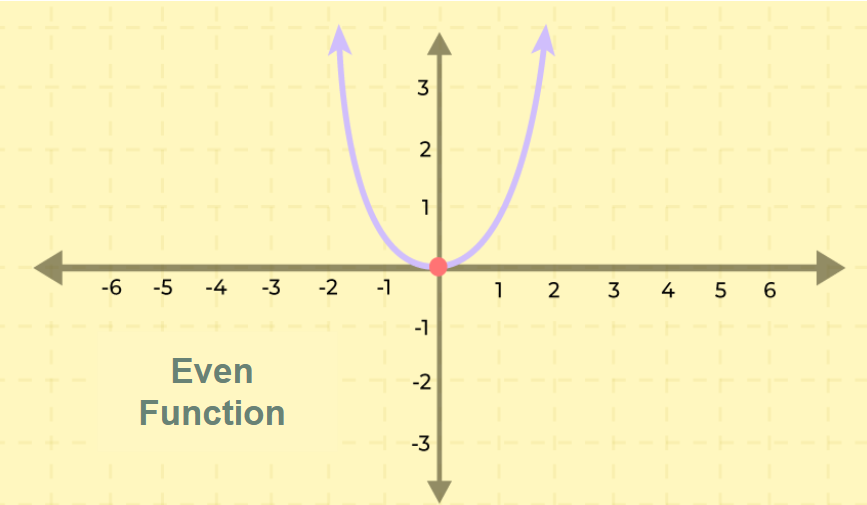
Odd Function

When all values of x and −x in the domain of f satisfy the following equation, the function “f” is considered odd:

-f(x) = f(-x)

Here, “Odd” is symmetric in that the graphical function would remain unchanged if it were rotated 180 degrees around the origin.

Odd Function Examples

Examples of odd functions includes:

• sin x
• x³, x⁵, x⁷, x⁹,…, i.e. xⁿ is an odd function when n is an odd integer
• x

Odd Functions Graph

An Odd function’s graph is symmetric concerning the origin that lies at the same distance from the origin but faces different directions. Whereas the function has opposite y values for any two opposite input values of x.

Neither Odd Nor Even

If a real-valued function f(x) does not fulfill f(-x) = f(x) and f(-x) = -f(x) for at least one value of x in the function’s domain, it is considered to be neither even nor odd (x). Suppose

f(x) = 2x⁵ + 3x² + 1

f(-x) = 2(-x)⁵ + 3(-x)² + 1

f(-x) = -2x⁵– 3x² + 1

(Both conditions failed)

Therefore, f(x) = 2x⁵ + 3x² + 1 is neither “Even” nor “Odd” Function.

Even and Odd Functions in Trigonometry

Six trigonometric ratios are:

• Sine Ratio
• Cosine Ratio
• Tangent Ratio
• Cotangent Ratio
• Secant Ratio
• Cosecant Ratio

Now for these trigonometric functions,

• All six of the trigonometric ratios have positive values in the first quadrant, which is where all of the x and y coordinates are positive.
• Only sine and cosecant have positive values in the second quadrant.
• Tangent and cotangent are positive in the third quadrant.
• Secant and cosine are positive in the fourth quadrant.

Properties of Even and Odd Functions

Some of the properties of Even and Odd Functions are given below.

• Only function that has an odd and even domain made up entirely of real numbers is the constant function, f(x) = 0, which is exactly zero.
• It is even to add two even functions and odd to add two odd functions. i.e.
  • Even Function + Even Function = Even Function
  • Odd Function + Odd Function = Odd Function
• When two even functions are separated, the difference is even, and when two odd functions are separated, the difference is odd.
• Unless one of the functions is a zero function, the sum of an even and an odd function is neither even nor odd.
• Both the product of two odd functions and the product of two even functions are even.
• Both the quotient of two odd functions and the quotient of two even functions are even.
• When two even functions are combined, they become even, and when two odd functions are combined, they become odd.

Integral Properties of Even and Odd Functions

Integrals over symmetric intervals can be made simpler by using the distinct integral features of even and odd functions. These are as follows:

Even Functions

When f(x) is an even function, its integral over the symmetric interval [−a, a] can be reduced as follows:

∫^a_-a f(x) dx = 2 ∫^a₀ f(x) dx

Due to its symmetry about the y-axis, the graph of an even function has this property. Integrating over a symmetric interval effectively doubles the area under the curve on one side, so we only need to compute half of it.

Odd Functions

When f(x) is an odd function, its integral over the symmetric interval [−a, a] can be reduced as follows:

∫^a_-a f(x) dx = 0

The rotational symmetry of the odd function’s graph origin gives birth to this characteristic. The net area is zero when the integration across a symmetric interval eliminates the positive and negative regions.

Read More

• Types of Function
• Function
• Trigonometric Functions

Even and Odd Functions Examples

Example 1: Using the notion of even and odd functions, ascertain if the function f(x) = Cosh(x) is even or not.

Solution:

Given Function:

• f(x) = Cosh(x)

f(x) = f(-x) for all x in its domain

Cosh(x) = Cosh (-x)

Cosh(-x) = Cosh (x)

Cosh(x), satisfies the condition f(x) = f(-x)

So, therefore, Cosh(x) is an even function

Example 2: Identify whether the function f(x) = x⁴ + 2x² -3 is even, odd, or neither.

Solution:

For Even Function:

Let’s take f(-x)

f(-x) = (-x)⁴ +2(-x)² – 3

f(-x) = x⁴ + 2x² – 3

Since, f(x) = f(-x),

Therefore, function f(x) is even.

Practice Questions on Even and Odd Functions

Question 1: Determine if the function g(x) = 1/x² is even, odd, or neither.

Question 2: Identify whether the function f(x) = x³+ x is even, or odd or neither.

Question 3: Identify if the function m(x) = e^x + e^-x is even, odd, or neither.

FAQs on Even and Odd Functions

What is Odd and Even Function?

If f(x) = f(−x) for any x in their domain, even functions are symmetric around the y-axis. Odd functions are symmetric about the origin, meaning that for every x in their domain, f(−x) = −f(x).

How can you tell if a function is even or odd?

A function is even if f(-x) = f(x), and odd if f(-x) = -f(x) for every element in the domain of f. If it doesn’t satisfy either property, it is neither odd nor even.

What are some examples of Odd Functions?

Some examples of odd functions are:

• f(x) = x³
• f(x) = sin(x)
• f(x) = 1/x

What are some examples of Even Functions?

Some examples of odd functions are:

• f(x) = x³
• f(x) = cos (x)
• f(x) = |x|

Can functions be neither Even nor Odd?

A function is neither even nor odd if it does not meet the requirements for being either. Instances comprise either linear functions such as f(x) = x or exponential functions such as f(x) = e^x.