Effect of Bias in Neural Network
Last Updated :
25 Sep, 2018
Neural Network is conceptually based on actual neuron of brain. Neurons are the basic units of a large neural network. A single neuron passes single forward based on input provided.
In Neural network, some inputs are provided to an artificial neuron, and with each input a weight is associated. Weight increases the steepness of activation function. This means weight decide how fast the activation function will trigger whereas bias is used to delay the triggering of the activation function.
For a typical neuron, if the inputs are x1, x2, and x3, then the synaptic weights to be applied to them are denoted as w1, w2, and w3.
Output is
y = f(x) = Σxiwi
where i is 1 to the number of inputs.
The weight shows the effectiveness of a particular input. More the weight of input, more it will have impact on network.
On the other hand Bias is like the intercept added in a linear equation. It is an additional parameter in the Neural Network which is used to adjust the output along with the weighted sum of the inputs to the neuron. Therefore Bias is a constant which helps the model in a way that it can fit best for the given data.
The processing done by a neuron is thus denoted as :
output = sum (weights * inputs) + bias
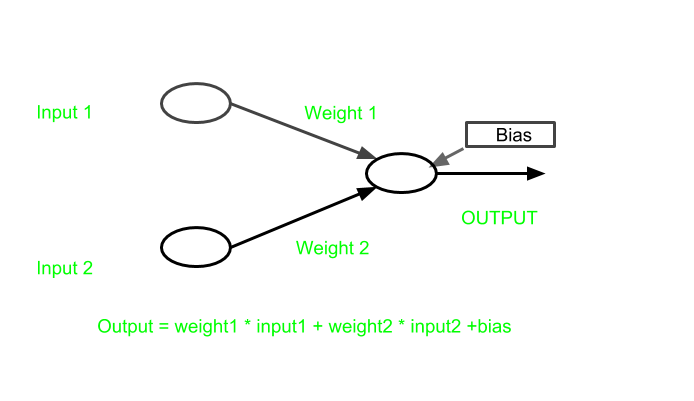
Need of bias
In above figure
y = mx+c
where
m = weight
and
c = bias
Now, Suppose if c was absent, then the graph will be formed like this:

Due to absence of bias, model will train over point passing through origin only, which is not in accordance with real-world scenario. Also with the introduction of bias, the model will become more flexible.
For Example:
Suppose an activation function act() which get triggered on some input greater than 0.
Now,
input1 = 1
weight1 = 2
input2 = 2
weight2 = 2
so
output = input1*weight1 + input2*weight2
output = 6
let
suppose act(output) = 1
Now a bias is introduced in output as
bias = -6
the output become 0.
act(0) = 0
so activation function will not trigger.
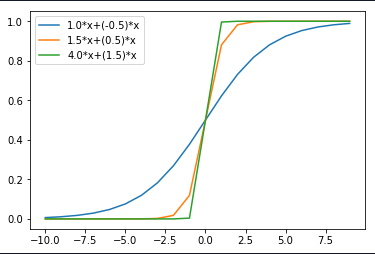
Change in weight
Here in graph, as it can be seen that when:
- weight WI
changed from 1.0 to 4.0
- weight W2
changed from -0.5 to 1.5
On increasing the weight the steepness is increasing.
Therefore it can be inferred that
More the weight earlier activation function will trigger.
Change in bias
Here in graph below, when
Bias changed from -1.0 to -5.0
The change in bias is increasing the value of triggering activation function.
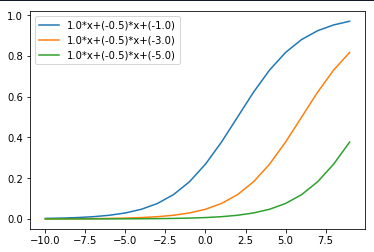
Therefore it can be inferred that from above graph that,
bias helps in controlling the value at which activation function will trigger.
Share your thoughts in the comments
Please Login to comment...