Drift Velocity as the name suggests refers to the slow movement of electrons in the conductor when an emf is introduced. Electrons do not move in a straight line in the conductor, but they move randomly in the conductor colliding with the other electrons and atoms exchanging energy, this exchange of energy moves forward in the direction opposite to the current and made the flow of electricity possible.
Drift Velocity Definition
Drift velocity is called the same because of the slow drift-like movement of electrons in the direction opposite to the electric field, also under the influence of the electric field thermal velocities between two collisions are high. The drift velocity refers to the average velocity obtained by a particle, such as an electron, as a result of an electric field’s action. Because the movement or motion of the particle is believed to be in a plane, axial drift velocity can be used to describe the motion.
Drift velocity is defined as “Average velocity with which the free electrons get drifted towards the positive end of the conductor under the influence of an external electric field.”
Net Velocity of Electrons
The random motion of free electrons moving around in the conductor can also be used to understand drift velocity. The electrons continue to move randomly as a result of this field, but their random motion will shift them toward a higher potential. This indicates that the electrons are drifting toward the conductor’s higher potential end. As a result, each electron will have a net velocity toward the conductor’s end. The Drift current is the current generated by the motion of electrons inside a conductor.
Because of collisions with other particles in the conductor, charged particles moving around in a conductor do not move in a straight line. As a result, the average particle speed in the conductor is considered. The drift velocity is the word for this.
- The drift velocity of electrons is in the order of 10-4 ms-1.
- The external electric field applied to the conductor setup is if V is the potential difference applied across the ends of the conductor of length l.
E = Potential Difference / Length
E = V / l
Drift Velocity Formula
The formula for Drift Velocity is given as follows:
vd = -eEτ / m
Where,
- vd is the drift velocity ,
- e is the charge of a electron,
- E is the strenth of electric feild,
- τ is the average relexatation time,
- m is the mass of electron
Drift Velocity Derivation
As each free electron in the conductor experiences a force,
F = -eE
and the acceleration of each electron is
a = F / m
From both the above equations, we get
∴ a = -eE / m (where m is the mass of the electron)
At any instant of time, the velocity acquired by an electron having thermal velocity u1 will be given using v = u + at as,
v1 = u1 + aτ1
Where,
- τ1 is Time taken by Electron to collide with Positive Ion
- v1 is Initial Velocity
Similarly, velocity acquired by electron, v2 = u2 + aτ2 , v2 = u2 + aτ2 , . . . . . . , vn = un + aτn
The average velocity of all the free electrons in the conductor under the effect of the external electric field is the drift velocity vd of the free electrons.
vd = ( v1 + v2 + . . . . + vn ) / n
⇒ vd = ((u1 + aτ1) + (u2 + aτ2) + . . . . + (un + aτn)) / n
⇒ vd = ((u1 + u2 + . . . +un)/n) + a((τ1 + τ2 + . . . . . + τn) /n) . . . (1)
when an Electric field is not applied to the conductor then there is no current in the conductor.
∴ (( u1 + u2 + . . . + un )/n) =0 . . . (2)
Putting equation 2 in equation 1, we get
vd = 0 + aτ [where τ = ((τ1 + τ2 + . . . . . + τn) /n)]
where τ is the average relaxation time and it refers to the length each electron takes to recover from its most recent interaction with a conductor atom.
we know, a = -eE / m [from force experienced by charge in an electric field]
∴ vd = -eEτ / m
where the negative sign shows the opposite direction of the electric field.
Drift Velocity, vd = eEτ / m …(3)
Alternate Formula for Drift Velocity
If the length of the conductor and time taken by the electron to travel throughout the length of the conductor is given then drift velocity can be calculated using the following formula
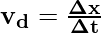
- Due to the frequent collisions that electrons have, their drift velocity is small.
- If the cross-section is constant, i ∝ J i.e. for a given cross-section area, the greater the current density, the larger will be current.
- In the presence of an exceptionally large number of free electrons in a conductor, a tiny amount of drift velocity produces a large amount of electric current.
- The electric bulb glows immediately when the switch is turned on because current transmission is practically as fast as light and involves electromagnetic processes.
- In the presence of an electric field, the path of electrons between successive collision are curved and In the absence of an electric field, the path of electrons between successive collision is a straight line.
- Free electron density in metal is
n = (NA × d) / A
Where,
- NA is Avogadro number
- x is number of free electrons per atom
- d is density of metal
- A is Atomic weight
Relaxation time (τ)
The time interval between two successive collisions of electrons with the positive ions in the metallic lattice is defined as relaxation time.
τ = mean free path / r.m.s. velocity of electrons
τ = λ / vrms
Thus, τ is inversely proportional to vrms
Mobility (μ)
Electron mobility is defined as “drift velocity per unit electric field.”
μ = vd / E
The unit of Mobility is m2 / volt-sec and using the above formula ohm’s law can be explained in terms of drift velocity as,
vd = μE
The magnitude of charge drift velocity per unit electric field applied is specified as the mobility of the charge carrier responsible for current.
μ = drift velocity / Electric field
⇒ μ = vd / E
⇒ μ = (eEτ / m) / E [from equation 3]
Thus, mobility of electron,
μ = eτ / m
Relation between Current and Drift velocity
As we know that current (I) is the rate of flow of charge.
i.e., I = Q / t . . . (a)
Let, length of wire = l, Area of cross-section = A, Number of electron volume = n, Drift velocity = vd
In simple, vd = l / t
∴ t = l / vd . . .(b)
As A is the cross-sectional area and l is the length of the conductor,
Thus, volume of conductor = A × l
If n is the number density of electrons, i.e the number of free electrons per unit volume of the conductor,
Number of free electrons in conductor = A × l × n
The total charge on all the free electrons in the conductor,
Charge(Q) = Number of electron × charge of each electron
∴ Q = A × l × n × e . . .(c)
As a result of this field, the free electrons in the conductor will begin to drift to the left, as indicated in the diagram below.
Using eq(a), eq(b), and eq(c).
I= (A × l × n × e) / (l/vd)
∴ I = A × l × n × e × vd / l
∴ I = A × n × e × vd . . . (p)
The average velocity gained by the free electrons of the conductor, which the electrons get drift under the influence of the electric field is given as,
∴ vd = I / A × n × e . . .(q)
Which is the required relation between current and drift velocity.
Putting the value of Average drift velocity vd = eEτ / m in eq (q)
I = A × n × e2 × τ × E / m
Relation between Current Density and Drift velocity
The current density is defined as ” The whole current supplying throughout a cross-sectional conductor unit within a unit of time.
I= A × n × e × vd . . .(o)
∴ J = I /A . . . (oo)
Put equation (oo) in equation (o),
J = A × n × e × vd / A
J = nevd
Where,
- J is the density of current
- A is tthe Area of cross-section
- n is the number of free electrons in volume
- vd is the Drift velocity
- e is charge of a electron
Therefore, as the current density is some constant multiple times the drift velocity so the electron velocity and its current density are equivalent to each other.
Important facts about Drift velocity
Various facts about drift velocities are,
- When an electric field is applied across a conductor, the electrons shift towards the high potential end of the wire.
- The current flowing in a conductor is directly proportional to the drift velocity of electrons.
- Unless an electric field is provided to the conductor, the electrons inside it move at random velocities and in random directions.
- Drift velocity is directly proportional to current and inversely proportional to r2.
Read More,
Sample Problems on Drift Velocity
Problem 1: The drift velocity of a free electron in a conductor is v when a current I is flowing in it. If both the radius and current are doubled, then the drift velocity will be?
Given: vd1 = v, i1 = i, i2 = 2i, r1 = r, r2 = 2r
To Find: vd2
Solution:
We know, i = A × n × e × vd
∴ vd = i / A × n × e
∴ vd = i / (πr2) × n × e
Drift velocity is directly proportional to current and inversely proportional to r2.
∴ vd1 / vd2 = (i1 / i2) × (r1 / r2)2
∴ vd1 / vd2 = (i / 2i) × (r / 2r)2
∴ v / vd2 = 1/2 × 4
∴ v / vd2 = 2
∴ vd2 = v / 2
∴ drift velocity is v / 2.
Problem 2: A conductor wire having 1029 free electrons/m3 carries a current of 20 A. If the cross-section of the wire is 1 mm2, then the drift velocity of the electron will be? (e = 1.6 x 10-19 C)
Given: n = 1029 m-3, i = 20A, A = 1 mm2 = 10-6 m2, e = 1.6 × 10-19 C
To Find: vd
Solution:
We know, i = A × n × e × vd
∴ vd = i / A × n × e
∴ vd = 20 / 10-6 × 1029 × 1.6 × 10-19
∴ vd = 1.25 × 10-3 m/s
Problem 3: A copper wire has a cross-sectional area of 7.85 x 10-7 m2. The number density of copper is 8.5 x 1028 m-3. Calculate the mean drift velocity of the electrons through the wire when the current is 1.4 A.
Given: A = 7.85 × 10-7 m2 , i= 1.4 A, n = 8.5 × 1028 m-3 , e = 1.6 × 10-19
To Find: Mean Drift Velocity
Solution:
We know, I = nAvde
∴ mean drift velocity = vd = I/(nAe)
∴ vd = 1.4 / 8.5 × 1028 × 7.85 × 10-7 × 1.6 × 10-19
∴ vd = 1.31 × 10-4 m/s
Problem 4: When a potential difference V is applied across a conductor at a temperature T, the drift velocity of electrons is proportional to?
Solution:
We know that,
Drift velocity vd = eEτ / m
∴ vd = (e × (V/l) × τ) / m …(E = V/l)
so for a particular conductor of a particular length the drift velocity will directly depend upon voltage. Hence, vd α V.
Problem 5: The resistivity of silver (ρ) = 1.54 × 10-8 Ωm, Electric field along the wire(E) = 1 volt/cm or 100 volts/m, The carrier concentration of electron (n) = 5.8 × 1028 m-3. Find the mobility of the electron and drift velocity.
Answer:
Solution:
μ = σ /ne
∴ μ = 1 / ρne …(σ = 1/ ρ)
∴ μ = 1/ 1.54 × 10-8 × 5.8 × 1028 × 1.6 × 10-19
∴ μ = 6.9973 × 10-3 m2/v/s
We know, μ = vd / E
∴ vd = μE
∴ vd = 6.9973 × 10-3 × 100
∴ vd = 0.69973 m/s
Drift velocity = 0.69973 m/s
FAQs on Drift Velocity
Q1: What is meant by Drift Velocity?
Answer:
Drift velocity is defined as “The Average velocity with which the free electrons get drifted towards the positive end of the conductor under the influence of an external electric field.”
Q2: What is the Formula for Drift Velocity?
Answer:
Formula for drift velocity is given by,
vd = -eEτ / m
Other than this, one realtion between current and drift velocity is
I = A × n × e × vd
Q3: How to find Drift Velocity?
Answer:
We can find drift velocity using the formula I = A × n × e × vdI where I is the current, A is the cross-sectional area of conductor, e is the charge of electron and vd is the drift velocity.
Q4: What is τ(Tau) in Drift Velocity?
Answer:
τ(tau) in drift velocity is the relexatation time, which is the average time between two collisions.
Q5: Explain the Relaxation time.
Answer:
“The time interval between two successive collisions of electrons with the positive ions in the metallic lattice is defined as relaxation time.”
τ = mean free path / r.m.s. velocity of electrons
τ = λ / vrms
Q6: Is Drift Velocity depends on the Diameter of the conductor?
Answer:
Drift velocity does not depend on the cross-sectional area or the diameter of any conductor. For the same potential difference here, with V across the conductor, an increase in the cross-sectional area decreases the resistance R=(ρ.l) / (A), And so, increasing the current i=V/R.
Share your thoughts in the comments
Please Login to comment...