Divisors in Maths

Divisor are one of the components in the division algorithm. Divisor is the number from which we divide the dividend to determine the quotient and remainder. In arithmetic, division is one of the four fundamental operations and other operations are addition, subtraction, and multiplication.

Divisors in Number Theory are defined a little differently, as any integer that divides another integer without leaving the remainder is also called a divisor. Divisors are the hidden helpers in the world of mathematics. They silently shape the foundation of all the numbers.

In this article, we will discuss both definitions of a divisor, including the general, early-class version and the definition in number theory. We will also explore various properties and examples related to divisors and discuss concepts such as prime divisors, the number of divisors, the sum of divisors, and the difference between a divisor and a factor. Let’s begin our exploration of this fundamental concept of divisors.

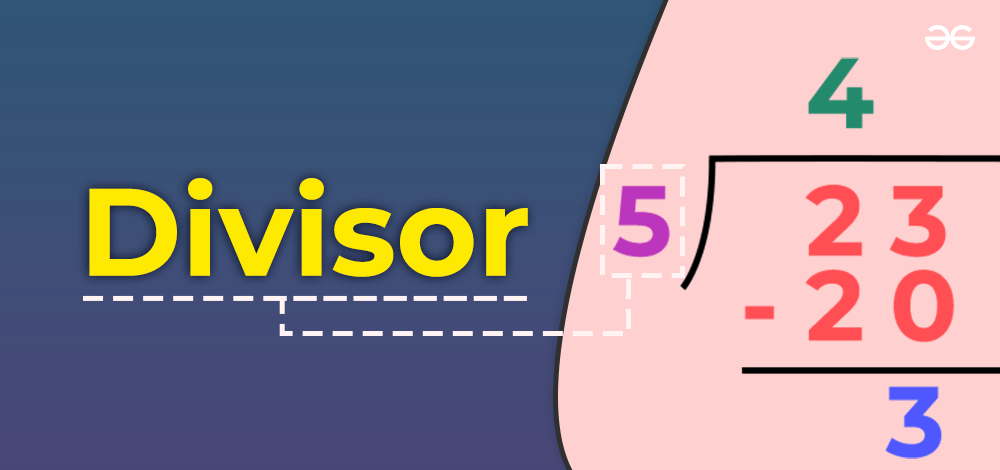
What are Divisors?

Divisors are integers (whole numbers) that are used to evenly divide another number without leaving a remainder. For example, the divisors of the number 16 are 1,2,4,8, and 16 because they evenly divide 16 without leaving any remainder. Whereas, 3 is not a divisor of the number 16 because when you divide 16 by 3, you get a remainder (16 ÷ 3 = 5).

Divisors play a fundamental role that is frequently used in various areas of mathematics such as number theory, algebra, arithmetic, and problem-solving situations.

Divisor Definition

Divisor is a number by which another number, known as the dividend, is divided.

In other words, a divisor is an integer that, when multiplied by a whole number, results in the original number without any fractional or remainder part.

Properties of Divisors

Here are some interesting properties of divisors:

• A divisor can never be 0 i.e., any number with 0 as its divisor is undefined. For example: If 2 is divided by 0 then the remainder will be 0 (2 ÷ 0 = not defined).
• A divisor can be positive or negative. However, if stated otherwise, the term is often restricted to positive integers.
• If a divisor has the same value as a dividend, the quotient will always be 1.
• An even number always has an even divisor. An odd number will always have an odd divisor.
• If a divisor is a decimal number, it should be converted into a whole number before dividing.

Divisors and Dividends

The key differences between both divisors and dividends are listed in the following table:

Characterstics	Divisors	Dividends
Definition	The number that divides another number is known as a divisor.	The dividend is the number that is divided into equal parts
Expression	In x ÷ y, “y” is the divisor	In x ÷ y, “x” is the dividend

In other words, a divisor is a factor of a dividend. For instance:

For 12 ÷ 4 = 3

• The divisor in this expression is 4
• The dividend in this expression is 12
• The quotient/remainder in this expression is 3.

Read more about Dividend, Quotient and Remainder.

Divisors vs Factors

The key difference between divisors and factors are:

Characterstics	Divisors	Factors
Definition	The number that divides another number is known as a divisor. In maths, sometimes divisors refer to the integers that evenly divide the number without leaving a remainder.	Factors are numbers that can be multiplied together to obtain a given number.
Example for 12	Divisors of 12: 1, 2, 3, 4, 6, 12	Factors of 12: 1, 2, 3, 4, 6, 12, -1, -2, -3, -4, -6, -12

Let’s consider an example, 15 divided by 5 gives 3 (15 ÷ 5 = 3). Similarly, if we divide 15 by 3 it gives 5 (15 ÷ 3 = 5).

The factors and divisors of 15 are 1, 3, 5 and 15 respectively.

However, if we divide 15 by 2 it will not completely divide the number. Thus, 2 is not the factor of 15 but will be considered a divisor.

Divisor in Number Theory

Number theory is a branch of pure mathematics devoted primarily to the study of integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) famously said that “mathematics is the queen of the sciences and number theory is the queen of mathematics.”

In number theory, a divisor is defined as a positive integer that evenly divides another integer without leaving a remainder. For example. the divisors of the number 35 are 1, 5, 7 and 35 because each number can divide the number, leaving no remainder.

How to Find Divisors of a Number?

There are a few ways to find out divisors of a number:

Brute Force Method: List out all the factors of the number, beginning with 1 and itself. For example, the divisors of 20 are 1, 2, 4, 5, 10, and 20.

Divisor Using Prime Factorization: Prime Factorization of a number involves expressing a positive integer as a product of its prime divisors. Prime numbers are those that have only 2 factors i.e. 1 and themselves.

For example, 20 can be written as follows:

20 = 5 × 4

Here, 5 is a prime number and 4 is a composite number, which can have more factors.

Thus, 20 = 2 × 2 × 5

Hence, the prime factorization of 20 is 2 × 2 × 5.

Examples of Divisors

As we already discussed in number theory, divisors are those positive integers that can evenly divide into another natural number without leaving a remainder. In other words, if you have an integer “n,” its divisors are the integers that, when multiplied by another integer, result in “n” without a remainder. Some examples of divisors for various natural numbers are discussed as below:

Divisors of 60

A number is a divisor of 60 if it divides 60 completely. Thus, x is a divisor of 60 if 60 divided by x is an integer. We have:

60/1 = 60	Pair 1: 1, 60
60/2 = 30	Pair 2: 2, 30
60/3=20	Pair 3: 3, 20
60/4=15	Pair 4: 4, 15
60/5=12	Pair 5: 5, 12
60/6=10	Pair 6: 6,10

Thus all the divisors for 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60. So, it is concluded that 60 has a total of twelve divisors.

Divisors of 72

A number is a divisor of 72 if it divides 72 completely. Thus, x is a divisor of 72 if 72 divided by x is an integer. We have:

72/1 = 70	Pair 1: 1, 70
72/2 = 36	Pair 2: 2, 36
72/3 = 24	Pair 3: 3, 24
72/6 = 12	Pair 4: 6, 12
72/8 = 9	Pair 5: 8, 9

Thus all the divisors for 60 are 1, 2, 3, 4, 6, 8, 9, 12, 24, 36 and 72. So, it is concluded that 60 has a total of eleven divisors.

Divisors of 18

A number is a divisor of 18 if it divides 18 completely. Thus, x is a divisor of 18 if 18 divided by x is an integer. We have

18/1 = 18	Pair 1: 1, 18
18/2 = 9	Pair 2: 2, 9
18/3 = 6	Pair 3: 3, 6
18/6 = 3	Pair 4: 6, 3

Thus all the divisors for 60 are 1, 2, 3, 6, 9 and 18. So, it is concluded that 18 has a total of six divisors.

Some other examples of divisors includes:

• The divisors of 12 are 1, 2, 3, 4, 6, and 12.
• The divisors of 20 are 1, 2, 4, 5, 10, and 20.
• The divisors of 7 are 1 and 7.
• The divisors of 16 are 1, 2, 4, 8, and 16.
• The divisors of 25 are 1, 5, and 25.
• The divisors of 9 are 1, 3, and 9.
• The divisors of 1 are 1.
• The divisors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100.
• The divisors of 33 are 1, 3, 11, and 33.
• The divisors of 50 are 1, 2, 5, 10, 25, and 50.

Special Case: Divisors of Zero

All positive and negative integers are divisors of 0. This is because it can be evenly divided by any integer. In other words, any integer n divides 0 without leaving a remainder, so n is a divisor of 0. They are —4, —5, 0, 1, 2, 3, and so on.

What are Prime Divisors?

Prime divisors are prime integers (whole numbers) that divide a given integer leaving no remainder. A prime divisor has at least two factors i.e 1 and itself. Below are some examples of prime divisors:

• Prime divisors of 14 are 2 and 7.
• Prime divisors of 18 are 2 and 3.
• Prime divisors of 30 are 2 and 3.
• Prime divisors of 49 are 7.
• Prime divisors of 60 are 2, 3, and 5.
• Prime divisors of 72 are 2 and 3.
• Prime divisors of 91 are 7 and 13.
• Prime divisors of 100 are 2 and 5.
• Prime divisors of 121 are 11.

Prime Divisors of 144

Let’s learn how to calculate prime divisors of number 144 using prime factorization method.

Step 1: Take the number 144 and and divide it with the smallest prime factor 2

• 144 ÷ 2 = 72

Step 2: Again divide 72 by the smallest prime factor 2 as 72 is divisible by 2 and continue the process

• 72 ÷ 2 = 36
• 36 ÷ 2 = 18
• 18 ÷ 2 = 9

Step 3: Now, 9 is not completely divisible by 2 as it will give a fractional number. Let’s divide it with the next smallest prime factor 3

• 9 ÷ 3 = 3
• 3 ÷ 3 = 1

Thus, we have a remainder 1. We cannot proceed further.

So, the prime divisors of number 144 are 2 × 2 × 2 × 2 × 3 × 3 or 24 × 32

Read more about Prime Numbers

Prime and Composite Divisors

Prime divisors are prime integers (whole numbers) that divide a given integer leaving no remainder. A prime divisor has at least two factors i.e 1 and itself.

Example: Let’s take 3. 3 is a prime number because it can only be divided by itself and 1.

So, the prime divisors of number 3 are 3 and 1.

• 3 ÷ 1 = 3
• 1 ÷ 3 = 3

Greatest Common Divisor

Greatest Common Divisor refers to the greatest number that is a common divisor for the given set of numbers. In other words, GCD is a greatest positive number which is a common factor of both the positive integers. 

Let’s find out the GCD of (13,46)

• Divisors of 13 = 1 and 13
• Divisors of 46 = 1,2,23 and 46

The common divisor of 13 and 46 is 1.

Thus, GCD of 13 and 46 is 1.

Therefore, GCD (13,46) = 1

Read more about HCF and LCM.

Number of Divisors

The number of divisors, referred as d(n) of a positive integer n is the total of all the positive integers that evenly divide n without leaving a remainder. Let’s under this by taking an example.

For example, the divisors of 12 are 1,2,3,4,6 and 12. Therefore, the number of divisors of 12 is d(12) = 6

Number of Divisors Formula

Number of Divisors for any given number is calculated using the following formula:

d(n) = (x₁ + 1) (x₂ + 1) ………. (x_k + 1)

Where x_1, x₂, . . . x_k are the exponent raised to the prime factors of n.

Let’s consider an example for better understanding.

The prime factorization of 12 is 2² × 3. Therefore, the number of divisors of 12 are:

d(12) = (2 +1) (2+1) (1+1) = 6

Euler’s Totient Function

Euler’s totient function, denoted as ϕ(n), counts the positive integers less than or equal to n that are coprime with n. In other words, they share no common factors other than 1.

Euler’s Totient Function is calculated by using the following formula:

ϕ(n) = n × (1 – 1/p₁) × (1 – 1/p₂) × . . . × (1 – 1/p_k)

Where n = a^p1 × b^p2 × c^p3 × . . . × k^pk_.

Let’s understand this by taking examples.

Example 1: For n = 12, find the number of divisors.

Solution:

Prime factorization of 12 = 2² x 3

ϕ(12) = 12 ( 1 – ½ ) (1 – ⅓) = 12 ( ½ x ⅔) = 4

Therefore, 12 has 4 positive integers less than or equal to 12 that are relatively prime to 12: 1, 5, 7, and 11

Example 2: Find ϕ(20).

Solution:

Prime factorization of 20 = 2² x 5

ϕ(20) = 20 (1 – ½ ) (1 – ⅓) = 20 ( ½ x ⅘) = 8

Therefore, 20 has 8 positive integers less than or equal to 20 that are relatively prime to 20: 1, 3, 7, 9, 11, 13, 17 and 19.

Sum of Divisors

The sum of divisors of a positive integer n is denoted by σ(n), where σ is the Euler’s Totient Function. σ(n) is calculated by using the following formula:

σ(n) = 1 + n + ∑_{d|n, d≠1, d≠n} d

Where d is the divisor of n.

Let’s understand this by taking examples.

Example 1: For n = 6, find the sum of divisors.

Solution:

Divisors of 6 are: 1, 2, 3, 6

σ(n) = 1 + 2 + 3 + 6 = 12

Example 2: Find σ(15).

Solution:

Divisors of 15 are: 1, 2, 4, 8, 16

σ(n) = 1 + 2 + 4 + 8 + 16 = 31

Read More,

• Addition
• Subtraction
• Multiplication

Sample Problems on Divisors

Problem 1: Find all the Divisors of 14.

Solution:

• 1 x 14 = 14
• 2 x 7 = 14
• 7 x 2 = 14

The divisors of the number 14 are 1, 2, 7 and 14

Therefore, the number of divisors of 14 is 4.

Problem 2: Find all the Divisors of 24

Solution:

• 1 x 24 = 24
• 2 x 12 = 24
• 3 x 8 = 24
• 4 x 6 = 24
• 6 x 4 = 24

The factors of the number 24 are 1, 2, 3, 4, 6 and 24

Therefore, the number of divisors of 24 is 6.

Problem 3: Find prime divisors of 460

Solution:

Step 1: Take the number 460 and and divide it with the smallest prime factor 2

• 460 ÷ 2 = 230

Step 2: Again divide 230 by the smallest prime factor 2 as 230 is divisible by 2

• 230 ÷ 2 = 115

Step 3: Now, 115 is not completely divisible by 2 as it will give a fractional number. Let’s divide it with the next smallest prime factor 5

• 115 ÷ 5 = 23

Step 4: As 23 is itself a prime number as it can only be divided by itself and 1. We cannot proceed further.

Therefore, the prime divisors of number 460 are 2² x 5 x 23

Problem 4: Find the number of divisors of 48.

Solution:

It is calculated using the following formula:

d(n) = (x₁ + 1) (x₂ + 1) . . . (x_k + 1)

The prime factorization of 48 is 2⁴ x 3. Therefore, the number of divisors of 12 are:

⇒ d(48) = (4 +1) (1+1)

⇒ d(48) = 5 x 2

⇒ d(48) = 10

Therefore, there are 10 divisors of 48

Problem 5: Find the number of divisors of 1080

Solution:

It is calculated using the following formula:

d(n) = (x₁ + 1) (x₂ + 1) . . . (x_k + 1)

The prime factorization of 1080 is 2³ x 3³ x 5. Therefore, the number of divisors of 1080 are:

⇒ d(1080) = (3+1) (3+1) (1+1)

⇒ d(1080) = 4 × 4 × 2

⇒ d(1080) = 32

Therefore, there are 32 divisors of 1080

Problem 6: Find the sum of divisors of 52

Solution:

It is calculated using the following formula:

σ(n) = 1 + n + ∑_{d|n, d≠1, d≠n} d

The divisors of 52 are 1, 2, 4, 13, 26, and 52

⇒ σ(52)=1+52+(2+4+13+26)

⇒ σ(52)=53+2+4+13+26

⇒ σ(52)=98

Therefore, the sum of divisors of 52 is 98

Problem 7: Find the φ(60) using Euler’s Totient Function formula

Solution:

It is calculated using the following formula:

ϕ(n) = n × (1 – 1/p₁) × (1 – 1/p₂) × . . . × (1 – 1/p_k)

The prime factorization of 60 is 2² x 3 x 5

⇒ ϕ(60) = 60 x ( 1 – 1/2) x (1 – 1/3) x (1 – 1/5)

⇒ ϕ(60) = 60 (1/2) (2/3) (4/5)

⇒ ϕ(60) = 24

So, φ(60) = 24. There are 24 positive integers less than or equal to 60 that are relatively prime to 60.

Practise Problems on Divisors

Promblem 1: List all divisors of following.

• 12
• 20
• 48
• 42
• 144

Promblem 2: Find the sum of all the divisors of the number 28.

Promblem 3: Determine the number of divisors of 36.

Promblem 4: Calculate the sum of all the divisors of 120.

Promblem 5: How many divisors does the number 150 have?

Promblem 6: Find the sum of the divisors of 72.

Promblem 7: Determine the number of divisors of 144.

Promblem 8: Calculate the sum of the divisors of 210.

Promblem 9: How many divisors does the number 625 have?

Promblem 10: Find the sum of all the divisors of 90.

Divisors – FAQs

1. What is Divisor in Math?

Divisor in math is a number that divided another number evenly without leaving any remainder.

2. How to find Divisors of a Number?

There are 2 main ways to find out the divisors of a number:

1. Take out all the factors of the number i.e 1 and the number itself.
2. Use prime factorization method.

3. What are Divisors of 12?

• 1 x 12 = 12
• 2 x 6 = 12
• 3 x 4 = 12
• 4 x 3 = 12

Therefore, the divisors of the numbers 12 are 1, 2, 3, 4, and 12

4. What are 1 digit Divisors?

1 digit or single digit divisors are positive integers that range from 1 – 9 which are divisors of any given number.

5. What are Divisors of 36?

• 1 x 36 = 36
• 2 x 18 = 36
• 3 x 12 = 36
• 4 x 9 = 36
• 6 x 6 = 36

Therefore, the divisors of the numbers 36 are 1, 2, 3, 4, 6 and 36

6. What are Common Divisors?

Common divisors are also known as common factors that refers to the positive integers which evenly divided the given numbers without leaving any remainder. 

For example, let’s find the common divisors of 12 and 20

• Divisors of 12: 1, 2, 3, 4, 6 and 12
• Divisors of 24: 1, 2, 4, 5, 10 and 20

Common Divisors of 12 and 20 are 1, 2 and 4

7. What is a Proper Divisor?

A proper divisor of a number is a divisor other than the number itself. For example, the proper divisors of 12 are 1, 2, 3, 4, and 6.

8. What is the Greatest Common Divisor (GCD)?

The Greatest Common Divisor (GCD) is the largest positive integer that divides two or more numbers without leaving a remainder. It’s also known as the Greatest Common Factor (GCF).

9. What is a Perfect Number?

A perfect number is a positive integer that is equal to the sum of its proper divisors. The smallest perfect number is 6 (1 + 2 + 3 = 6).

10. What is an Abundant Number?

An abundant number is a positive integer for which the sum of its proper divisors is greater than the number itself. For example, 12 is an abundant number (1 + 2 + 3 + 4 + 6 = 16).

11. What is a Deficient Number?

A deficient number is a positive integer for which the sum of its proper divisors is less than the number itself. For example, 8 is a deficient number (1 + 2 + 4 = 7).

12. Can Zero be a Divisor?

No, zero cannot be a divisor. Division by zero is undefined in mathematics.