Divisible by 37 for large numbers

Given a large number n, we need to check whether it is divisible by 37. Print true if it is divisible by 37 otherwise False.
Examples:

Input  : 74
Output : True

Input : 73
Output : False

Input : 8955795758 (10 digit number)
Output : True

A r digit number m whose digital form is (ar-1 ar-2….a2 a1 a0) is divisible by 37 if and only if the sum of series of numbers (a2 a1 a0) + (a5 a4 a3) + (a8 a7 a6) + … is divisible by 37. The triplets of digits within parenthesis represent 3-digit number in digital form.

The given number n can be written as a sum of powers of 1000 as follows. 
n = (a2 a1 a0) + (a5 a4 a3)*1000 + (a8 a7 a6)*(1000*1000) +…. 
As 1000 = (1)(mod 37), 1000 as per congruence relation. 
For a positive integer n, two numbers a and b are said to be congruent modulo n, if their difference 
(a – b) is an integer multiple of n (that is, if there is an integer k such that a – b = kn). This congruence relation is typically considered when a and b are integers, and is denoted

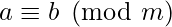
Hence we can write: 
n = { (a2a1a0) + (a5a4a3)* (1) + (a8a7a6)* (1)*(1)+…..}(mod 37), 
Thus n is divisible by 37 if and if only if the series is divisible by 37.

Examples:

Input : 8955795758 (10 digit number)
Output : True
Explanation:
     We express the number in terms of 
     triplets of digits as follows.
     (008)(955)(795)(758)
     Now, 758 + 795 + 955 + 8 = 2516
     For 2516, the triplets will be:
     (002)(516)
     Now 516 + 2 = 518 which is divisible 
     by 37. Hence the number is divisible 
     by 37.

Input : 189710809179199 (15 digit number)
Output : False

A simple and efficient method is to take input in form of string (make its length in form of 3*m by adding 0 to left of number if required) and then you have to add the digits in blocks of three from right to left until it become a 3 digit number to form an series . Calculate the sum of the series. If the sum of series has more than 3 digits in it, again recursively call this function. 
Finally check whether the resultant sum is divisible by 37 or not.
Here is the program implementation to check divisibility by 37.

C++

// CPP program for checking divisibility by 37
// function divisible37 which returns True if
// number is divisible by 37 otherwise False
#include <bits/stdc++.h>
using namespace std;

int divisibleby37(string n){
    int l = n.length();
    if (n == "0")
        return 0;

    // Append required 0's at the beginning
    if (l % 3 == 1){
        n = "00"+ n;
        l += 2;
    }
    else if (l % 3 == 2){
        n = "0"+ n;
        l += 1;
    }

    int gSum = 0;

    while (l != 0){

    // group saves 3-digit group
    string group = n.substr(l - 3, l);
        l = l - 3;
    int gvalue = (group[0] - '0') * 100 +
                 (group[1] - '0') * 10 +
                 (group[2] - '0') * 1;

    // add the series
    gSum = gSum + gvalue;
    }

    // if sum of series gSum has minimum 4
    // digits in it, then again recursive
    // call divisibleby37 function
    if (gSum >= 1000)
        return (divisibleby37(to_string(gSum)));
    else
        return (gSum % 37 == 0);

}

// driver program to test the above function
int main(){

    string s="8955795758";

    if (divisibleby37(s))
    cout<<"True";
    else
    cout<<"False";
    return 0;
}
// This code is contributed by Prerna Saini

Java

// Java program for checking
// divisibility by 37

class GFG
{
// function divisible37 which
// returns True if number is
// divisible by 37 otherwise False
static int divisibleby37(String n1)
{
    int l = n1.length();
    if (n1 == "0")
        return 0;

    // Append required 0's
    // at the beginning
    if (l % 3 == 1)
    {
        n1 = "00"+ n1;
        l += 2;
    }
    else if (l % 3 == 2)
    {
        n1 = "0"+ n1;
        l += 1;
    }
    char[]  n= n1.toCharArray();
    int gSum = 0;
    while (l != 0)
    {

    // group saves 3-digit group
    int gvalue;
    if(l == 2)
        gvalue = ((int)n[(l - 2)] - 48) * 100 +
                ((int)n[(l - 1)] - 48) * 10;
    else if(l == 1)
        gvalue = ((int)n[(l - 1)] - 48) * 100;
    else
        gvalue = ((int)n[(l - 3)] - 48) * 100 +
                ((int)n[(l - 2)] - 48) * 10 +
                ((int)n[(l - 1)] - 48) * 1;
    l = l - 3;

    // add the series
    gSum = gSum + gvalue;
    }

    // if sum of series gSum has minimum 4
    // digits in it, then again recursive
    // call divisibleby37 function
    if (gSum >= 1000)
        return (divisibleby37(String.valueOf(gSum)));
    else
        return (gSum % 37 == 0) ? 1 : 0;

}

// Driver Code
public static void main(String[] args)
{
    String s="8955795758";

    if (divisibleby37(s) == 1)
    System.out.println("True");
    else
    System.out.println("False");
}
}

// This code is contributed by mits

Python3

# Python code for checking divisibility by 37
# function divisible37 which returns True if
# number is divisible by 37 otherwise False
def divisibleby37(n):
    l = len(n)
    if (n == 0):
        return True

    # Append required 0's at the beginning
    if (l%3 == 1):
        n = "00"+ n
        l += 2
    elif (l%3 == 2):
        n = "0"+ n
        l += 1

    gSum = 0
    while (l != 0):

        # group saves 3-digit group
        group = int(n[l-3:l])
        l = l-3

        # add the series
        gSum = gSum + group

    # if sum of series gSum has minimum 4
    # digits in it, then again recursive
    # call divisibleby37 function
    if (gSum >= 1000):
        return(divisibleby37(str(gSum)))
    else:
        return (gSum%37==0)

# Driver method to test the above function
print(divisibleby37("8955795758"))

C#

// C# program for checking
// divisibility by 37
using System;

class GFG
{
// function divisible37 which
// returns True if number is
// divisible by 37 otherwise False
static int divisibleby37(string n)
{
    int l = n.Length;
    if (n == "0")
        return 0;

    // Append required 0's
    // at the beginning
    if (l % 3 == 1)
    {
        n = "00"+ n;
        l += 2;
    }
    else if (l % 3 == 2)
    {
        n = "0"+ n;
        l += 1;
    }

    int gSum = 0;
    while (l != 0)
    {

    // group saves 3-digit group
    int gvalue;
    if(l == 2)
        gvalue = ((int)n[(l - 2)] - 48) * 100 +
                 ((int)n[(l - 1)] - 48) * 10;
    else if(l == 1)
        gvalue = ((int)n[(l - 1)] - 48) * 100;
    else
        gvalue = ((int)n[(l - 3)] - 48) * 100 +
                 ((int)n[(l - 2)] - 48) * 10 +
                 ((int)n[(l - 1)] - 48) * 1;
    l = l - 3;

    // add the series
    gSum = gSum + gvalue;
    }

    // if sum of series gSum has minimum 4
    // digits in it, then again recursive
    // call divisibleby37 function
    if (gSum >= 1000)
        return (divisibleby37(gSum.ToString()));
    else
        return (gSum % 37 == 0) ? 1 : 0;

}

// Driver Code
public static void Main()
{
    string s="8955795758";

    if (divisibleby37(s) == 1)
    Console.WriteLine("True");
    else
    Console.WriteLine("False");
}
}

// This code is contributed by mits

PHP

<?php
// PHP program for checking
// divisibility by 37

// function divisible37 which
// returns True if number is
// divisible by 37 otherwise
// False
function divisibleby37($n)
{
    $l = strlen($n);
    if ($n == '0')
        return 0;

    // Append required 0's
    // at the beginning
    if ($l % 3 == 1)
    {
        $n = "00" . $n;
        $l += 2;
    }
    else if ($l % 3 == 2)
    {
        $n = "0" . $n;
        $l += 1;
    }

    $gSum = 0;

    while ($l != 0)
    {

    // group saves 3-digit group
    $group = substr($n,$l - 3, $l);
        $l = $l - 3;
    $gvalue = (ord($group[0]) - 48) * 100 +
              (ord($group[1]) - 48) * 10 +
              (ord($group[2]) - 48) * 1;

    // add the series
    $gSum = $gSum + $gvalue;
    }

    // if sum of series gSum has
    // minimum 4 digits in it,
    // then again recursive call
    // divisibleby37 function
    if ($gSum >= 1000)
        return (divisibleby37((string)($gSum)));
    else
        return ($gSum % 37 == 0);

}

// Driver code
$s = "8955795758";

if (divisibleby37($s))
echo "True";
else
echo "False";

// This code is contributed
// by mits
?>

Javascript

<script>
// Javascript program for checking
// divisibility by 37

// function divisible37 which
// returns True if number is
// divisible by 37 otherwise
// False
function divisibleby37(n)
{
    let l = n.length;
    if (n == '0')
        return 0;

    // Append required 0's
    // at the beginning
    if (l % 3 == 1)
    {
        n = "00" + n;
        l += 2;
    }
    else if (l % 3 == 2)
    {
        n = "0" + n;
        l += 1;
    }

    let gSum = 0;

    while (l != 0)
    {

    // group saves 3-digit group
    let group = n.substr(l - 3, l);
        l = l - 3;
    gvalue = (group.charCodeAt(0) - 48) * 100 +
             (group.charCodeAt(1) - 48) * 10 +
             (group.charCodeAt(2) - 48) * 1;

    // add the series
    gSum = gSum + gvalue;
    }

    // if sum of series gSum has
    // minimum 4 digits in it,
    // then again recursive call
    // divisibleby37 function
    if (gSum >= 1000)
        return (divisibleby37(`${gSum}`));
    else
        return (gSum % 37 == 0);

}

// Driver code
let s = "8955795758";

if (divisibleby37(s))
    document.write("True");
else
    document.write("False");

// This code is contributed
// by _saurabh_jaiswal.
</script>

Output

True

Time Complexity: O(n), where n is the length of the string.
Auxiliary Space: O(1)

Method: Checking given number is divisible by 37 or not by using modulo division operator “%”.

C++

// C++ code To check whether the given number is divisible
// by 37 or not

#include <iostream>
using namespace std;

int main()
{

    // input number
    int num = 8955;
    // checking if the given number is divisible by 37 or
    // not using modulo division operator if the output of
    // num%37 is equal to 0 then given number is divisible
    // by 37 otherwise not divisible by 37
    if (num % 37 == 0) {
        cout << " divisible";
    }
    else {
        cout << " not divisible";
    }
    return 0;
}

Java

// Java code To check whether the given number is divisible
// by 37 or not
import java.util.*;

class GFG
{
  public static void main(String[] args)
  {

    // input number
    int num = 8955;

    // checking if the given number is divisible by 37 or
    // not using modulo division operator if the output of
    // num%37 is equal to 0 then given number is divisible
    // by 37 otherwise not divisible by 37
    if (num % 37 == 0) {
      System.out.println(" divisible");
    }
    else {
      System.out.println(" not divisible");
    }
  }
}

// This code is contributed by phasing17

Python3

# Python code
# To check whether the given number is divisible by 37 or not

#input
n=8955795758
# the above input can also be given as n=input() -> taking input from user
# finding given number is divisible by 37 or not
if int(n)%37==0:
  print("true")
else:
  print("false")

  # this code is contributed by gangarajula laxmi

C#

using System;

public class GFG {

    static public void Main()
    {

        // input number
        long num = 8955795758;

    // checking if the given number is divisible by 37 or
    // not using modulo division operator if the output of
    // num%37 is equal to 0 then given number is divisible
    // by 37 otherwise not divisible by 37
        if (num % 37 == 0) {
            Console.Write("Yes");
        }
        else {
            Console.Write("No");
        }
    }
}

// This code is contributed by laxmigangarajula03

Javascript

<script>
        // JavaScript code for the above approach
        // To check whether the given number is divisible by 37 or not

        // input
        var n = 8955795758

        // finding given number is divisible by 37 or not
        if (n % 37 == 0)
            document.write("true")
        else
            document.write("false")

 // This code is contributed by laxmigangarajula03
    </script>

PHP

<?php
    $num = 8955795758;
    // checking if the given number is divisible by 37 or
    // not using modulo division operator if the output of
    // num%37 is equal to 0 then given number is divisible
    // by 37 otherwise not divisible by 37
    if ($num % 37 == 0) {
        echo "true";
    }
    else {
        echo "false";
    }

?>

Output

true

Time Complexity: O(1) 
Auxiliary Space: O(1)