Differential or Derivatives in MATLAB
Last Updated :
23 Aug, 2021
Differentiation of a function y = f(x) tells us how the value of y changes with respect to change in x. It can also be termed as the slope of a function.
Derivative of a function f(x) wrt to x is represented as 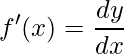
MATLAB allows users to calculate the derivative of a function using diff() method. Different syntax of diff() method are:
- f’ = diff(f)
- f’ = diff(f, a)
- f’ = diff(f, b, 2)
f’ = diff(f)
It returns the derivative of function f(x) wrt variable x.
Example 1:
Matlab
syms x
f = cos(x);
disp("f(x) :");
disp(f);
d = diff(f);
disp("Derivative of f(x) :");
disp(d);
|
Output :

Example 2: Evaluating the derivative of a function at a specified value using subs(y,x,k).
- subs(y,x,k), it gives the value of function y at x = k.
Matlab
# variable x
syms x
f = cos(x);
disp("f(x) :");
disp(f);
d = diff(f);
val = subs(d,x,pi/2);
disp("Value of f'(x) at x = pi/2:");
disp(val);
|
Output :
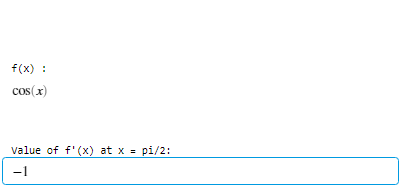
f’ = diff(f, a)
- It returns the derivative of function f with respect to variable a.
Matlab
syms x t;
f = sin(x*t);
disp("f(x) :");
disp(f);
d = diff(f,t);
disp("Derivative of f(x,t) wrt t:");
disp(d);
|
Output :
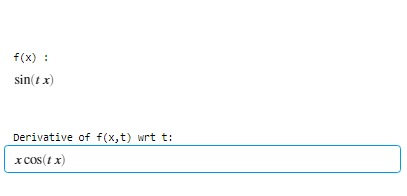
f’ = diff(f, b, 2)
It returns the double derivative of function f with respect to variable b.
Example 1:
Matlab
syms x n;
f = x^n;
disp("f(x,n) :");
disp(f);
d = diff(f,x,2);
disp("Double Derivative of f(x,n) wrt x:");
disp(d);
|
Output :

In the same way, you can also calculate the k-order derivative of function f using diff(f,x,k).
Example 2:
Calculating the partial derivative 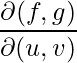 } using Jacobian matrix and determinant.
} using Jacobian matrix and determinant.
Matlab
syms u v;
f = u^2;
g = sin(v)*(3*u);
disp("f(u,v) :");
disp(f);
disp("g(u,v) :");
disp(g);
J = jacobian([f; g], [u v]);
disp("Jacobian matrix :");
disp(J);
d = det(J);
disp("Determinant of Jacobian matrix:");
disp(d);
|
Output :

Share your thoughts in the comments
Please Login to comment...