Different ways to represent N as sum of K non-zero integers
Last Updated :
23 May, 2022
Given N and K. The task is to find out how many different ways there are to represent N as the sum of K non-zero integers.
Examples:
Input: N = 5, K = 3
Output: 6
The possible combinations of integers are:
( 1, 1, 3 )
( 1, 3, 1 )
( 3, 1, 1 )
( 1, 2, 2 )
( 2, 2, 1 )
( 2, 1, 2 )
Input: N = 10, K = 4
Output: 84
The approach to the problem is to observe a sequence and use combinations to solve the problem. To obtain a number N, N 1’s are required, summation of N 1’s will give N. The problem allows you to use K integers only to make N.
Observation:
Let's take N = 5 and K = 3, then all
possible combinations of K numbers are: ( 1, 1, 3 )
( 1, 3, 1 )
( 3, 1, 1 )
( 1, 2, 2 )
( 2, 2, 1 )
( 2, 1, 2 )
The above can be rewritten as: ( 1, 1, 1 + 1 + 1 )
( 1, 1 + 1 + 1, 1 )
( 1 + 1 + 1, 1, 1 )
( 1, 1 + 1, 1 + 1 )
( 1 + 1, 1 + 1, 1 )
( 1 + 1, 1, 1 + 1 )
From above, a conclusion can be drawn that of N 1’s, k-1 commas have to be placed in between N 1’s and the remaining places are to be filled with ‘+’ signs. All combinations of placing k-1 commas and placing ‘+’ signs in the remaining places will be the answer. So, in general, for N there will be N-1 spaces between all 1, and out of those choose k-1 and place a comma in between those 1. In between the rest 1’s, place ‘+’ signs. So the way of choosing K-1 objects out of N-1 is 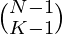 . The dynamic programming approach is used to calculate
. The dynamic programming approach is used to calculate 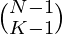 .
.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int binomialCoeff(int n, int k)
{
int C[n + 1][k + 1];
int i, j;
for (i = 0; i <= n; i++) {
for (j = 0; j <= min(i, k); j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
return C[n][k];
}
int main()
{
int n = 5, k = 3;
cout << "Total number of different ways are "
<< binomialCoeff(n - 1, k - 1);
return 0;
}
|
C
#include <stdio.h>
int min(int a, int b)
{
int min = a;
if(min > b)
min = b;
return min;
}
int binomialCoeff(int n, int k)
{
int C[n + 1][k + 1];
int i, j;
for (i = 0; i <= n; i++) {
for (j = 0; j <= min(i, k); j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
return C[n][k];
}
int main()
{
int n = 5, k = 3;
printf("Total number of different ways are %d",binomialCoeff(n - 1, k - 1));
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int binomialCoeff(int n,
int k)
{
int C[][] = new int [n + 1][k + 1];
int i, j;
for (i = 0; i <= n; i++)
{
for (j = 0;
j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
return C[n][k];
}
public static void main (String[] args)
{
int n = 5, k = 3;
System.out.println( "Total number of " +
"different ways are " +
binomialCoeff(n - 1,
k - 1));
}
}
|
Python3
def binomialCoeff(n, k):
C = [[0 for i in range(k+1)]for i in range(n+1)]
for i in range(0,n+1,1):
for j in range(0,min(i, k)+1,1):
if (j == 0 or j == i):
C[i][j] = 1
else:
C[i][j] = C[i - 1][j - 1] + C[i - 1][j]
return C[n][k]
if __name__ == '__main__':
n = 5
k = 3
print("Total number of different ways are",binomialCoeff(n - 1, k - 1))
|
C#
using System;
class GFG
{
static int binomialCoeff(int n,
int k)
{
int [,]C = new int [n + 1,
k + 1];
int i, j;
for (i = 0; i <= n; i++)
{
for (j = 0;
j <= Math.Min(i, k); j++)
{
if (j == 0 || j == i)
C[i, j] = 1;
else
C[i, j] = C[i - 1, j - 1] +
C[i - 1, j];
}
}
return C[n,k];
}
public static void Main ()
{
int n = 5, k = 3;
Console.WriteLine( "Total number of " +
"different ways are " +
binomialCoeff(n - 1,
k - 1));
}
}
|
PHP
<?php
function binomialCoeff($n, $k)
{
$C = array(array());
$i; $j;
for ($i = 0; $i <= $n; $i++)
{
for ($j = 0;
$j <= min($i, $k); $j++)
{
if ($j == 0 or $j == $i)
$C[$i][$j] = 1;
else
$C[$i][$j] = $C[$i - 1][$j - 1] +
$C[$i - 1][$j];
}
}
return $C[$n][$k];
}
$n = 5; $k = 3;
echo "Total number of " ,
"different ways are " ,
binomialCoeff($n - 1,
$k - 1);
?>
|
Javascript
<script>
function binomialCoeff(n, k)
{
let C = new Array(n + 1);
for(let i = 0; i < n + 1; i ++)
{
C[i] = new Array(k + 1);
for(let j = 0; j < k + 1; j++)
{
C[i][j] = 0;
}
}
let i, j;
for (i = 0; i <= n; i++)
{
for (j = 0; j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
return C[n][k];
}
let n = 5, k = 3;
document.write( "Total number of " +
"different ways are " +
binomialCoeff(n - 1,
k - 1));
</script>
|
Output: Total number of different ways are 6
Time Complexity: O(N * K)
Auxiliary Space: O(N * K)
Share your thoughts in the comments
Please Login to comment...