Difference between Heaps and Sorted Array
Last Updated :
22 Apr, 2022
1. Heap:
A heap is a tree based data structure in which tree should be almost complete. It is of two types i.e. max and min heap.
- Max heap: In max heap, if p is the parent and c is its child, then for every parent p the value of it is greater than or equal to the value of c
- Min heap In min heap, if p is the parent and c is its child, then for every parent p value is less than or equal to the value of c.
Heap is also used as priority queue. In which highest(in case of max heap) or lowest(in case of min heap) element is present at the root.
Heap is used in problems where we need to remove the highest or lowest priority element. A common implementation of heap is binary heap.
Implementation
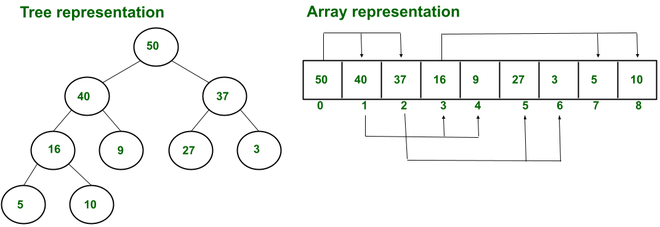
- Although heap can be implemented as a tree, but lots of storage will go waste for storing pointers. Due to the property of heap being a complete binary tree, it can be easily stored in an array.
- Where root element is stored at first index and its child index can be calculated as following.
- Left child index = 2×r where r is index of the root and array starting index is 1 .
- Right child index = 2×r+1.
- And parent index can be calculated as floor (i/2) where i is the index of its left or right child.
Example:
Example of Max heap
2. Sorted array:
A sorted array is a data structure in which elements are sorted in numerical, alphabetical, or by some other order and stored at contiguous memory locations.

Sorted array example
- All data structures have their own pros and cons depending on the problems or algorithms where they are used. For example heap is the best data structure in situations where we need optimality in finding (max or min frequently), deleting (max or min) or inserting (max or min) element.
- And sorted array is used in situations when items need to be stored in ascending or descending orders. For example: in shortest-job-first scheduling algorithms where the processes(stored in array) need to be sorted according to burst time of the processes. So in case sorting array is required.
| Data structure |
Insert |
Search |
Find min |
Delete min |
| Sorted array |
O(n) |
O(log n) |
O(1) |
O(n) |
| Min heap |
O(log n) |
O(n) |
O(1) |
O(log n) |
Difference between Heaps and Sorted Array:
|
Sorted array
|
Heaps
|
| In sorted array, elements are sorted in numerical, alphabetical, or by some other order and stored at contiguous memory locations. |
A heap is almost complete binary tree, In case of max heap, if p is the parent and c is its child, then the value of p is greater than or equal to the value of c and in min heap if p is the parent and c is its child, then the value p is less than or equal to the value of c. |
| A sorted array can act as heap when using array based heap implementation. |
Heap may or may not be a sorted array when using array based heap implementation. |
| For a given set of integers, there can be two arrangements (i.e. ascending or descending) possible after sorting . |
For a given set of n integers, multiple possible heaps (max or min) can be formed.
Refer this article for more details
|
| Here the next element address can be accessed by incrementing the index of current element. |
Here the left child index can be accessed by calculating 2×r and right element index can be accessed by calculating 2×r+1, where r is the index of root and array is 1 index based. |
| Searching can be performed in O(log n) time in sorted array by using binary search. |
Heap is not optimal for searching operation but searching can be performed in O(n) complexity. |
| Heap sort can be used for sorting an array, but for this first heap is build with array of n integers and then heap sort is applied. Here O(n) time complexity is needed for building heap and O(n log n) is required for removing n (min or max) element from heap and placing at the end of array and decreasing the size of array). |
Heap sort which is applied on heaps (min or max) and it is in-place sorting algorithm for performing sorting in O(n log n) time complexity. |
| Sorting an array requires O(n log n) complexity which is best time complexity for sorting an array of n items in comparison based sorting algorithm. |
Building heap takes O(n) time complexity. |
| Sorted array are used for performing efficient searching (i.e. binary search), SJFS scheduling algorithm and in the organizations where data is needed in sorted order etc. |
The heaps are used in heap sort, priority queue, graph algorithms and K way merge etc. |
Share your thoughts in the comments
Please Login to comment...