Difference between General tree and Binary tree
Last Updated :
19 Feb, 2020
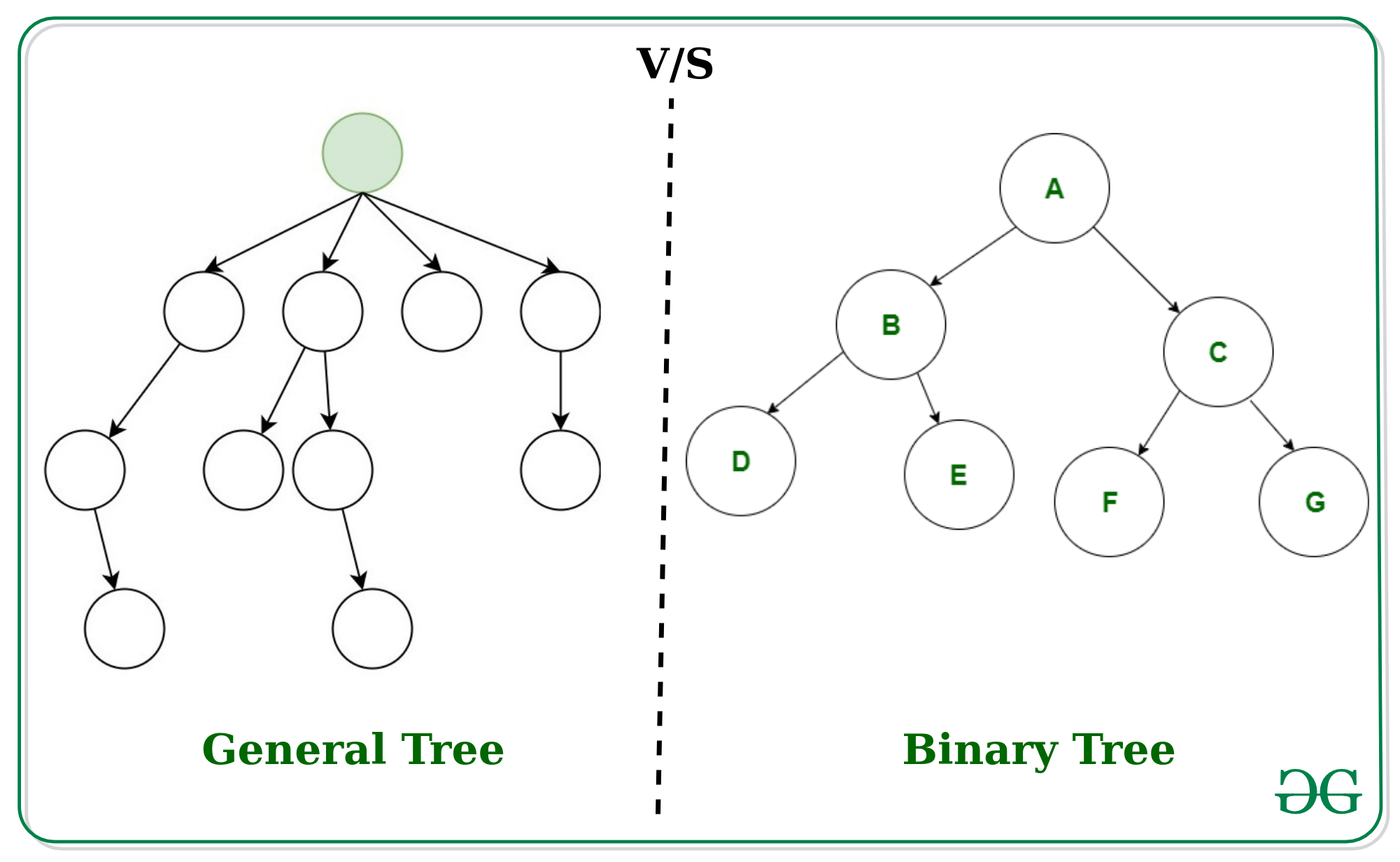
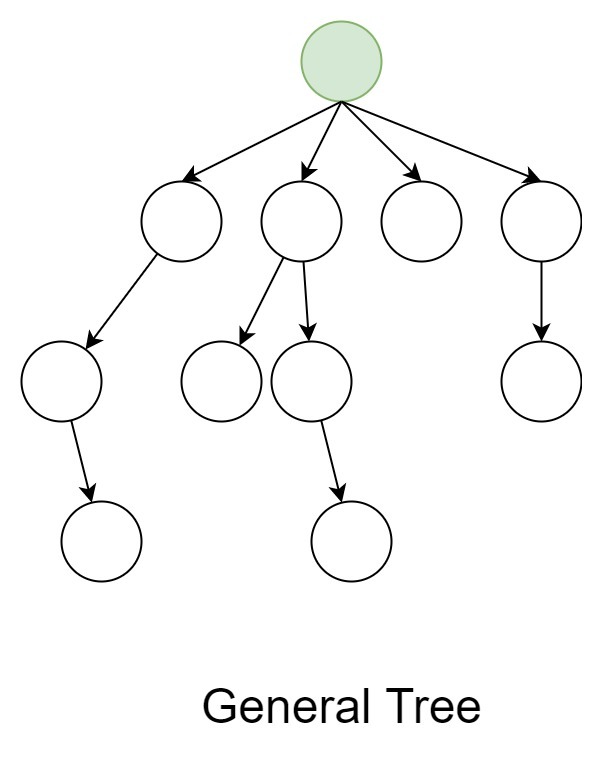
General Tree:
In the data structure, General tree is a tree in which each node can have either zero or many child nodes. It can not be empty. In general tree, there is no limitation on the degree of a node. The topmost node of a general tree is called the root node. There are many subtrees in a general tree. The subtree of a general tree is unordered because the nodes of the general tree can not be ordered according to specific criteria. In a general tree, each node has in-degree(number of parent nodes) one and maximum out-degree(number of child nodes) n.
Binary Tree:
A binary tree is the specialized version of the General tree. A binary tree is a tree in which each node can have at most two nodes. In a binary tree, there is a limitation on the degree of a node because the nodes in a binary tree can’t have more than two child node(or degree two). The topmost node of a binary tree is called root node and there are mainly two subtrees one is left-subtree and another is right-subtree. Unlike the general tree, the binary tree can be empty. Unlike the general tree, the subtree of a binary tree is ordered because the nodes of a binary tree can be ordered according to specific criteria.

Difference between General tree and Binary tree
| General tree |
Binary tree |
| General tree is a tree in which each node can have many children or nodes. |
Whereas in binary tree, each node can have at most two nodes. |
| The subtree of a general tree do not hold the ordered property. |
While the subtree of binary tree hold the ordered property. |
| In data structure, a general tree can not be empty. |
While it can be empty. |
| In general tree, a node can have at most n(number of child nodes) nodes. |
While in binary tree, a node can have at most 2(number of child nodes) nodes. |
| In general tree, there is no limitation on the degree of a node. |
While in binary tree, there is limitation on the degree of a node because the nodes in a binary tree can’t have more than two child node. |
| In general tree, there is either zero subtree or many subtree. |
While in binary tree, there are mainly two subtree: Left-subtree and Right-subtree. |
Share your thoughts in the comments
Please Login to comment...