Determine whether the given Array forms a valley or not

Given an array arr[] of length N, the task is to check whether the given array forms a valley or not. An array is said to be a valley if there is a point till which the array is non-increasing and after that increases in nature. Formally arr[0] ≥ arr[1] ≥ . . . ≥ arr[i] ≤ arr[i+1] ≤ . . . ≤ arr[N-1] and arr[0] > arr[i] and arr[i] < arr[N-1], where i is any index in the range [1, N-2].

Note: An array with only a single element is also considered to be a valley.

Input: N = 6  arr[] = {5, 4, 4, 3, 2, 2}
Output: No

Not a valley

Input: N = 8  arr[] = {5, 4, 4, 3, 4, 4, 5, 6}
Output: Yes

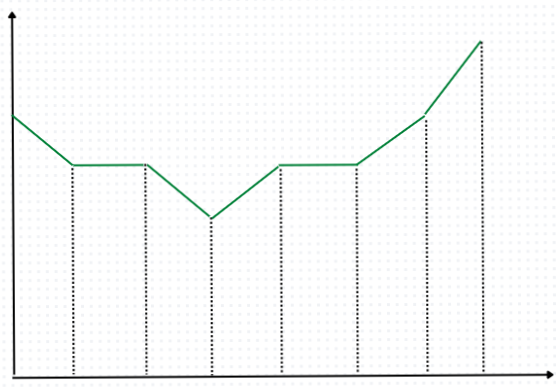
valley representing given input

Input: N = 5  arr[] = {4, 5, 5, 6, 4}
Output: No

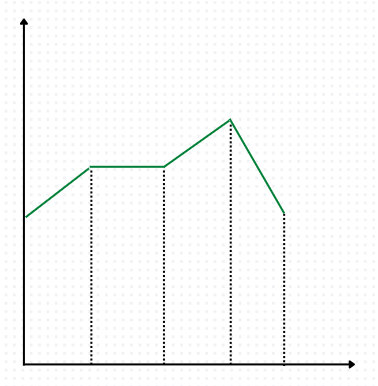
array doesn’t form a valley

Approach: The problem can be solved using linear iteration based  on the following idea:

Find any index i, such that all the elements before that are in non-increasing order and after that all the elements are in non-decreasing order.

Follow the steps to solve the problem:

• Traverse from the start to the index (say idx) where the current element becomes greater than the previous. 
• From that index traverse till the end and check if they are in non-decreasing order.
• Finally, check if arr[idx-1] is less than both arr[0] and arr[N-1].
• If the above conditions are satisfied, return “Yes”. Otherwise, the array does not form a valley.

Below is the code for the discussed approach:

C++

// C++ code to implement the approach

#include <bits/stdc++.h>
using namespace std;

// Function for checking if the given array
// forms a valley or not
int isValley(vector<int>& a, int n)
{
    int idx = 0;
    for (int i = 1; i < n; i++) {

        // Index where monoticity
        // of the given array changes
        if (a[i] > a[i - 1]) {
            idx = i;
            break;
        }
    }
    if (idx == 0)
        return 0;

    for (int i = idx + 1; i < n; i++) {
        if (a[i] < a[i - 1])
            return 0;
    }
    if (a[idx - 1] >= a[0] or a[idx - 1] >= a[n - 1])
        return 0;

    return 1;
}

// Driver Code
int main()
{
    vector<int> arr = { 5, 4, 4, 3, 2, 2 };
    int N = arr.size();

    int sol = isValley(arr, N);
    if (sol)
        cout << "Yes\n";
    else
        cout << "No\n";

    return 0;
}

Java

// Java code to implement the approach
import java.io.*;

class GFG {

  // Function for checking if the given array
  // forms a valley or not
  static boolean isValley(int[] a, int n)
  {
    int idx = 0;
    for (int i = 1; i < n; i++) {
      if (a[i] > a[i - 1]) {
        idx = i;
        break;
      }
    }
    if (idx == 0) {
      return false;
    }
    for (int i = idx + 1; i < n; i++) {
      if (a[i] < a[i - 1])
        return false;
    }
    if (a[idx - 1] >= a[0] || a[idx - 1] >= a[n - 1])
      return false;

    return true;
  }

  public static void main(String[] args)
  {
    int[] arr = { 5, 4, 4, 3, 2, 2 };
    int N = arr.length;

    boolean sol = isValley(arr, N);
    if (sol) {
      System.out.println("Yes");
    }
    else {
      System.out.println("No");
    }
  }
}

// This code is contributed by lokesh.

C#

// C# code to implement the approach
using System;

class GFG {

// Function for checking if the given array
// forms a valley or not
static bool isValley(int[] a, int n)
{
    int idx = 0;
    for (int i = 1; i < n; i++) {
    if (a[i] > a[i - 1]) {
        idx = i;
        break;
    }
    }
    if (idx == 0) {
    return false;
    }
    for (int i = idx + 1; i < n; i++) {
    if (a[i] < a[i - 1])
        return false;
    }
    if (a[idx - 1] >= a[0] || a[idx - 1] >= a[n - 1])
    return false;

    return true;
}

public static void Main()
{
    int[] arr = { 5, 4, 4, 3, 2, 2 };
    int N = arr.Length;

    bool sol = isValley(arr, N);
    if (sol) {
    Console.Write("Yes");
    }
    else {
    Console.Write("No");
    }
}
}

// This code is contributed by Pushpesh Raj.

Javascript

// JavaScript code to implement the approach

// Function for checking if the given array
// forms a valley or not
function isValley(a, n)
{
    let idx = 0;
    for (let i = 1; i < n; i++) {

        // Index where monoticity
        // of the given array changes
        if (a[i] > a[i - 1]) {
            idx = i;
            break;
        }
    }
    if (idx == 0)
        return 0;

    for (let i = idx + 1; i < n; i++) {
        if (a[i] < a[i - 1])
            return 0;
    }
    if (a[idx - 1] >= a[0] || a[idx - 1] >= a[n - 1])
        return 0;

    return 1;
}

// Driver Code

    let arr = [5, 4, 4, 3, 2, 2];
    let N = arr.length;

    let sol = isValley(arr, N);
    if (sol)
        console.log("Yes");
    else
        console.log("No");

// This code is contributed by poojaagarwal2.

Python3

# Python3 code for the above approach
# Function for checking if the given array forms a valley or not


def isValley(a, n):
    idx = 0
    # Index where monoticity of the given array changes
    for i in range(1, n):
        if a[i] > a[i - 1]:
            idx = i
            break

    if idx == 0:
        return 0

    for i in range(idx + 1, n):
        if a[i] < a[i - 1]:
            return 0

    if a[idx - 1] >= a[0] or a[idx - 1] >= a[n - 1]:
        return 0

    return 1


 # Driver Code
arr = [5, 4, 4, 3, 2, 2]
N = len(arr)

sol = isValley(arr, N)
if sol:
    print("Yes")
else:
    print("No")
#This code is contributed by Potta Lokesh

Output

No

Time Complexity: O(N)
Auxiliary Space: O(1)

My Personal Notes arrow_drop_up

Save