Test of Multicollinearity

Multicollinearity: It generally occurs when the independent variables in a regression model are correlated with each other. This correlation is not expected as the independent variables are assumed to be independent. If the degree of this correlation is high, it may cause problems while predicting results from the model.

Few Consequences of Multicollinearity

1. The estimators have high variances and covariances which makes precise estimation difficult.
2. Due to the above consequence in point 1, the confidence intervals tend to become wider which leads to the acceptance of the zero null hypothesis more often.
3. The standard errors can be sensitive to small changes in the data.
4. Coefficients become very sensitive to small changes in the model. It reduces the statistical power of the regression model.
5. The effects of a single variable become difficult to distinguish from the other variables.

Let us understand Multicollinearity with the help of an example:

Example: Steve jogs while listening to music. When he listens to music for longer he ends up jogging for longer. Now we want to determine the fitness of Steve. What can we say, which will have a greater impact on it? Listening to music or Jogging? We can’t actually tell because these estimators have an interdependency on each other. If we try to measure his fitness by listening to music he is also jogging at the same time and when we try to measure his fitness from jogging he is also listening to music. Since both the attributes were taken as estimators for his fitness it is difficult to get an accurate result due to the presence of Multicollinearity between these variables.

Variance Inflating factor (VIF) is used to test the presence of multicollinearity in a regression model. It is defined as,

For a regression model 

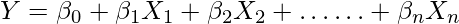
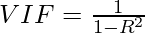
where,

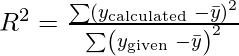
Measure of Multicollinearity

If the value of VIF is –

• 1 => not correlated. Multicollinearity doesn’t exist.
• Between 1 and 5 => moderately correlated. Low multicollinearity exists.
• Greater than 5 => Highly correlated. High Multicollinearity exists.

The inverse of VIF is called Tolerance and is given as –

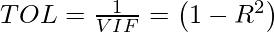
• When R² = 0 meaning no collinearity is present then we can say that the Tolerance is high (=1).

You can then use other techniques to resolve this issue of multicollinearity if the extent is too high.

For any queries leave a comment down below.