PyTorch in a lot of ways behaves like the arrays we love from Numpy. These Numpy arrays, after all, are just tensors. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation) and another module specifically for building neural networks. All together, PyTorch ends up being more flexible with Python and the Numpy stack compared to TensorFlow and other frameworks.
Neural Networks: Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply “neurons.” Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit’s output. Below is an example of a simple
PyTorch is an open-source machine learning library based on the Torch library, developed by Facebook’s AI Research lab. It is widely used in deep learning, natural language processing, and computer vision applications. PyTorch provides a dynamic computational graph, which allows for easy and efficient modeling of complex neural networks.
Here’s a general overview of how to use PyTorch for deep learning:
Define the model: PyTorch provides a wide range of pre-built neural network architectures, such as fully connected networks, convolutional neural networks (CNNs), and recurrent neural networks (RNNs). The model can be defined using PyTorch’s torch.nn module.
Define the loss function: The loss function is used to evaluate the model’s performance and update its parameters. PyTorch provides a wide range of loss functions, such as cross-entropy loss and mean squared error loss.
Define the optimizer: The optimizer is used to update the model’s parameters based on the gradients of the loss function. PyTorch provides a wide range of optimizers, such as Adam and SGD.
Train the model: The model is trained on a dataset using the defined loss function and optimizer. PyTorch provides a convenient data loading and processing library, torch.utils.data, that can be used to load and prepare the data.
Evaluate the model: After training, the model’s performance can be evaluated on a test dataset.
Deploy the model: The trained model can be deployed in a wide range of applications, such as computer vision and natural language processing.
neural net. 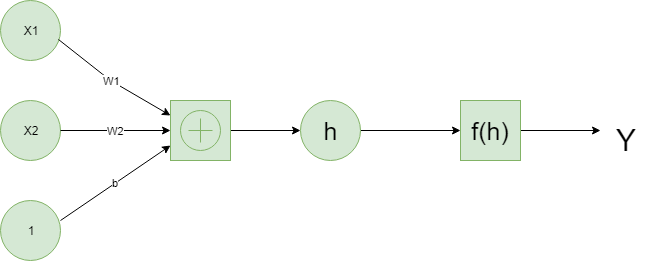
Tensors: It turns out neural network computations are just a bunch of linear algebra operations on tensors, which are a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor. The fundamental data structure for neural networks are tensors and PyTorch is built around tensors. It’s time to explore how we can use PyTorch to build a simple neural network.
Define an activation function(sigmoid) to compute the linear output
Python3
def activation(x):
return 1/(1 + torch.exp(-x))
|
Python3
features = torch.randn((1, 5))
weights = torch.randn_like(features)
bias = torch.randn((1, 1))
|
features = torch.randn((1, 5)) creates a tensor with shape (1, 5), one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one. weights = torch.randn_like(features) creates another tensor with the same shape as features, again containing values from a normal distribution. Finally, bias = torch.randn((1, 1)) creates a single value from a normal distribution.
Now we calculate the output of the network using matrix multiplication.
Python3
y = activation(torch.mm(features, weights.view(5, 1)) + bias)
|
That’s how we can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix. We define the structure of neural network and initialize the weights and biases.
Python3
features = torch.randn((1, 3))
n_input = features.shape[1]
n_hidden = 2
n_output = 1
W1 = torch.randn(n_input, n_hidden)
W2 = torch.randn(n_hidden, n_output)
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
|
Now we can calculate the output for this multi-layer network using the weights W1 & W2, and the biases, B1 & B2.
Python3
h = activation(torch.mm(features, W1) + B1)
output = activation(torch.mm(h, W2) + B2)
print(output)
|
ADVANTAGES AND DISADVANTAGES:
Advantages of using PyTorch for deep learning:
Dynamic computational graph: PyTorch’s dynamic computational graph allows for easy and efficient modeling of complex neural networks. This makes it well-suited for tasks such as natural language processing and computer vision.
User-friendly API: PyTorch has a user-friendly and intuitive API, which makes it easy to implement, debug, and experiment with different models.
Active community: PyTorch has a large and active community, which means that you can find a lot of tutorials, pre-trained models, and other resources to help you get started.
Integration with other libraries: PyTorch has great integration with other libraries such as CUDA, which allows for fast and efficient training of models on GPUs.
Easy to use for distributed training: PyTorch makes it easy to perform distributed training across multiple GPUs and machines, which can significantly speed up training time.
Disadvantages of using PyTorch for deep learning:
Less mature than TensorFlow: PyTorch is relatively new compared to TensorFlow, which means that it may have less mature libraries and fewer resources available.
Less production ready: PyTorch is more suited for research and development work, rather than for production-level deployment.
Less optimized for mobile: PyTorch does not have as good support for mobile deployment as TensorFlow Lite.
Less optimized for browser: PyTorch does not have as good support for browser deployment as TensorFlow.js
Less optimized for Autograd: PyTorch’s Autograd implementation is less optimized than TensorFlow’s, which can make training large models more memory-intensive.
REFERENCES:
Here are a few popular books on the topic of PyTorch and deep learning:
“PyTorch for Deep Learning: From Beginner to Pro” by Ankit Jain: This book provides a comprehensive introduction to PyTorch and deep learning. It covers the basics of PyTorch and deep learning, and provides hands-on examples of implementing various deep learning models using PyTorch.
“Deep Learning with PyTorch” by Eli Stevens, Luca Antiga, Thomas Viehmann: This book provides a hands-on approach to learning deep learning and PyTorch. It covers the basics of deep learning and PyTorch, and provides hands-on examples of implementing various deep learning models using PyTorch.
“Hands-On Machine Learning with PyTorch” by Gaurav Sharma : This book provides a hands-on approach to learning machine learning and PyTorch. It covers the basics of machine learning, deep learning and PyTorch, and provides hands-on examples of implementing various machine learning models using PyTorch.
“Programming PyTorch for Deep Learning” by Ian Pointer: This book provides a hands-on approach to learning deep learning with PyTorch. It covers the basics of PyTorch, deep learning, and provides hands-on examples of implementing various deep learning models using PyTorch.
Share your thoughts in the comments
Please Login to comment...