Cunningham Numbers
Last Updated :
10 Dec, 2021
Cunningham Number is a number N of the form  , where a, b >= 2.
, where a, b >= 2.
Few Cunningham numbers are:
3, 5, 7, 8, 9, 10, 15, 17, 24, 26, 28…
Check if N is a Cunningham number
Given a number N, the task is to check if N is an Cunningham Number or not. If N is an Cunningham Number then print “Yes” else print “No”.
Examples:
Input: N = 126
Output: Yes
Explanation:
126 = 5^3+1
Input: N = 16
Output: No
Approach: The idea is to solve the equation in a desired form such that checking that the number is a Cunningham Number or not is easy.
// Cunningham Numbers are the
// which can be represented as
=> 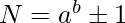 =>
=> 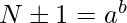
Therefore, if  or
or  can be expressed in the form of
can be expressed in the form of  , then the number is cunningham Number.
, then the number is cunningham Number.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPower(int a)
{
if (a == 1)
return true;
for (int i = 2; i * i <= a; i++) {
double val = log(a) / log(i);
if ((val - (int)val) < 0.00000001)
return true;
}
return false;
}
bool isCunningham(int n)
{
return isPower(n - 1) ||
isPower(n + 1);
}
int main()
{
int n = 126;
if (isCunningham(n))
cout << "Yes";
else
cout << "No";
return 0;
}
|
Java
import java.util.*;
class GFG{
static boolean isPower(int a)
{
if (a == 1)
return true;
for(int i = 2; i * i <= a; i++)
{
double val = Math.log(a) / Math.log(i);
if ((val - (int)val) < 0.00000001)
return true;
}
return false;
}
static boolean isCunningham(int n)
{
return isPower(n - 1) ||
isPower(n + 1);
}
public static void main (String[] args)
{
int n = 126;
if (isCunningham(n))
System.out.print("Yes");
else
System.out.print("No");
}
}
|
Python3
import math
def isPower(a):
if (a == 1):
return True
i = 2
while(i * i <= a):
val = math.log(a) / math.log(i)
if ((val - int(val)) < 0.00000001):
return True
i += 1
return False
def isCunningham(n):
return isPower(n - 1) or isPower(n + 1)
n = 126
if (isCunningham(n)):
print("Yes")
else:
print("No")
|
C#
using System;
class GFG{
static bool isPower(int a)
{
if (a == 1)
return true;
for(int i = 2; i * i <= a; i++)
{
double val = Math.Log(a) / Math.Log(i);
if ((val - (int)val) < 0.00000001)
return true;
}
return false;
}
static bool isCunningham(int n)
{
return isPower(n - 1) ||
isPower(n + 1);
}
public static void Main (string[] args)
{
int n = 126;
if (isCunningham(n))
Console.Write("Yes");
else
Console.Write("No");
}
}
|
Javascript
<script>
function isPower( a)
{
if (a == 1)
return true;
for ( let i = 2; i * i <= a; i++)
{
let val = Math.log(a) / Math.log(i);
if ((val - parseInt( val) < 0.00000001))
return true;
}
return false;
}
function isCunningham(n)
{
return isPower(n - 1) || isPower(n + 1);
}
let n = 126;
if (isCunningham(n))
document.write("Yes");
else
document.write("No");
</script>
|
Time Complexity: O(n1/2)
Auxiliary Space: O(1)
Reference: https://oeis.org/A080262
Share your thoughts in the comments
Please Login to comment...