Cross Validation in Machine Learning
Last Updated :
21 Dec, 2023
In machine learning, we couldn’t fit the model on the training data and can’t say that the model will work accurately for the real data. For this, we must assure that our model got the correct patterns from the data, and it is not getting up too much noise. For this purpose, we use the cross-validation technique. In this article, we’ll delve into the process of cross-validation in machine learning.
What is Cross-Validation?
Cross validation is a technique used in machine learning to evaluate the performance of a model on unseen data. It involves dividing the available data into multiple folds or subsets, using one of these folds as a validation set, and training the model on the remaining folds. This process is repeated multiple times, each time using a different fold as the validation set. Finally, the results from each validation step are averaged to produce a more robust estimate of the model’s performance. Cross validation is an important step in the machine learning process and helps to ensure that the model selected for deployment is robust and generalizes well to new data.
What is cross-validation used for?
The main purpose of cross validation is to prevent overfitting, which occurs when a model is trained too well on the training data and performs poorly on new, unseen data. By evaluating the model on multiple validation sets, cross validation provides a more realistic estimate of the model’s generalization performance, i.e., its ability to perform well on new, unseen data.
Types of Cross-Validation
There are several types of cross validation techniques, including k-fold cross validation, leave-one-out cross validation, and Holdout validation, Stratified Cross-Validation. The choice of technique depends on the size and nature of the data, as well as the specific requirements of the modeling problem.
1. Holdout Validation
In Holdout Validation, we perform training on the 50% of the given dataset and rest 50% is used for the testing purpose. It’s a simple and quick way to evaluate a model. The major drawback of this method is that we perform training on the 50% of the dataset, it may possible that the remaining 50% of the data contains some important information which we are leaving while training our model i.e. higher bias.
2. LOOCV (Leave One Out Cross Validation)
In this method, we perform training on the whole dataset but leaves only one data-point of the available dataset and then iterates for each data-point. In LOOCV, the model is trained on  samples and tested on the one omitted sample, repeating this process for each data point in the dataset. It has some advantages as well as disadvantages also.
samples and tested on the one omitted sample, repeating this process for each data point in the dataset. It has some advantages as well as disadvantages also.
An advantage of using this method is that we make use of all data points and hence it is low bias.
The major drawback of this method is that it leads to higher variation in the testing model as we are testing against one data point. If the data point is an outlier it can lead to higher variation. Another drawback is it takes a lot of execution time as it iterates over ‘the number of data points’ times.
3. Stratified Cross-Validation
It is a technique used in machine learning to ensure that each fold of the cross-validation process maintains the same class distribution as the entire dataset. This is particularly important when dealing with imbalanced datasets, where certain classes may be underrepresented. In this method,
- The dataset is divided into k folds while maintaining the proportion of classes in each fold.
- During each iteration, one-fold is used for testing, and the remaining folds are used for training.
- The process is repeated k times, with each fold serving as the test set exactly once.
Stratified Cross-Validation is essential when dealing with classification problems where maintaining the balance of class distribution is crucial for the model to generalize well to unseen data.
4. K-Fold Cross Validation
In K-Fold Cross Validation, we split the dataset into k number of subsets (known as folds) then we perform training on the all the subsets but leave one(k-1) subset for the evaluation of the trained model. In this method, we iterate k times with a different subset reserved for testing purpose each time.
Note: It is always suggested that the value of k should be 10 as the lower value of k is takes towards validation and higher value of k leads to LOOCV method.
Example of K Fold Cross Validation
The diagram below shows an example of the training subsets and evaluation subsets generated in k-fold cross-validation. Here, we have total 25 instances. In first iteration we use the first 20 percent of data for evaluation, and the remaining 80 percent for training ([1-5] testing and [5-25] training) while in the second iteration we use the second subset of 20 percent for evaluation, and the remaining three subsets of the data for training ([5-10] testing and [1-5 and 10-25] training), and so on. 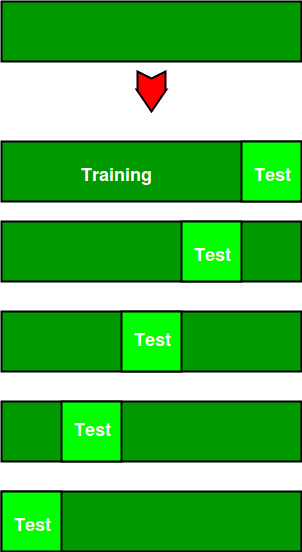
Total instances: 25
Value of k : 5
No. Iteration Training set observations Testing set observations
1 [ 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] [0 1 2 3 4]
2 [ 0 1 2 3 4 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] [5 6 7 8 9]
3 [ 0 1 2 3 4 5 6 7 8 9 15 16 17 18 19 20 21 22 23 24] [10 11 12 13 14]
4 [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 20 21 22 23 24] [15 16 17 18 19]
5 [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19] [20 21 22 23 24]
Comparison between cross-validation and hold out method
Advantages of train/test split:
- This runs K times faster than Leave One Out cross-validation because K-fold cross-validation repeats the train/test split K-times.
- Simpler to examine the detailed results of the testing process.
Advantages of cross-validation:
- More accurate estimate of out-of-sample accuracy.
- More “efficient” use of data as every observation is used for both training and testing.
Advantages and Disadvantages of Cross Validation
Advantages:
- Overcoming Overfitting: Cross validation helps to prevent overfitting by providing a more robust estimate of the model’s performance on unseen data.
- Model Selection: Cross validation can be used to compare different models and select the one that performs the best on average.
- Hyperparameter tuning: Cross validation can be used to optimize the hyperparameters of a model, such as the regularization parameter, by selecting the values that result in the best performance on the validation set.
- Data Efficient: Cross validation allows the use of all the available data for both training and validation, making it a more data-efficient method compared to traditional validation techniques.
Disadvantages:
- Computationally Expensive: Cross validation can be computationally expensive, especially when the number of folds is large or when the model is complex and requires a long time to train.
- Time-Consuming: Cross validation can be time-consuming, especially when there are many hyperparameters to tune or when multiple models need to be compared.
- Bias-Variance Tradeoff: The choice of the number of folds in cross validation can impact the bias-variance tradeoff, i.e., too few folds may result in high variance, while too many folds may result in high bias.
Python implementation for k fold cross-validation
Step 1: Import necessary libraries.
Python3
from sklearn.model_selection import cross_val_score, KFold
from sklearn.svm import SVC
from sklearn.datasets import load_iris
|
Step 2: Load the dataset
let’s use the iris dataset, a multi-class classification in-built dataset.
Python3
iris = load_iris()
X, y = iris.data, iris.target
|
Step 3: Create SVM classifier
SVC is a Support Vector Classification model from scikit-learn.
Python3
svm_classifier = SVC(kernel='linear')
|
Step 4:Define the number of folds for cross-validation
Python3
num_folds = 5
kf = KFold(n_splits=num_folds, shuffle=True, random_state=42)
|
Step 5: Perform k-fold cross-validation
Python3
cross_val_results = cross_val_score(svm_classifier, X, y, cv=kf)
|
Step 6: Evaluation metrics
Python3
print(f'Cross-Validation Results (Accuracy): {cross_val_results}')
print(f'Mean Accuracy: {cross_val_results.mean()}')
|
Output:
Cross-Validation Results (Accuracy): [1. 1. 0.96666667 0.93333333 0.96666667]
Mean Accuracy: 0.9733333333333334
Frequently Asked Questions(FAQs)
1.What is K in K fold cross validation?
It represents the number of folds or subsets into which the dataset is divided for cross-validation. Common values are 5 or 10.
2.How many folds for cross-validation?
The number of folds is a parameter in K-fold cross-validation, typically set to 5 or 10. It determines how many subsets the dataset is divided into.
3.What is cross-validation example?
Split the dataset into five folds. For each fold, train the model on four folds and evaluate it on the remaining fold. The average performance across all five folds is the estimated out-of-sample accuracy.
4.What is the purpose of validation?
Validation assesses a model’s performance on unseen data, helping detect overfitting. It ensures the model generalizes well and is not just memorizing the training data.
5. Why use 10-fold cross-validation?
10-fold cross-validation provides a balance between robust evaluation and computational efficiency. It offers a good trade-off by dividing the data into 10 subsets for comprehensive assessment.
Share your thoughts in the comments
Please Login to comment...