Count triangles required to form a House of Cards of height N
Last Updated :
17 Mar, 2021
Given a number N, the task is to count the number of triangles required to form a House of Cards of N levels.
Examples:
Input: N = 3
Output: 13
Explanation:

From the above image, the following observations can be made:
Count of triangles of unit 1 = 9 (6 non-inverted triangles and 3 inverted triangles)
Count of triangles of unit 2 = 3
Count of triangles of unit 3 = 1
Therefore, total number of triangles = 6 + 3 + 3 + 1 = 13
Input: N = 2
Output: 5
Approach: The required number of triangles required to form a House of Cards of N levelscan be calculated by the formula:
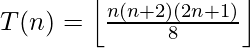
Illustration:
For N = 3
Count of triangles = 3 * (3 + 2) * (6 + 1) / 8 = 13
For N = 2
Count of triangles = 2 * (2 + 2) * (4+ 1) / 8 = 5
Below is the implementation of the above approach:
CPP
#include <bits/stdc++.h>
using namespace std;
int noOfTriangles(int n)
{
return floor(n * (n + 2)
* (2 * n + 1) / 8);
}
int main()
{
int n = 3;
cout << noOfTriangles(n) << endl;
return 0;
}
|
Java
import java.lang.*;
class GFG {
public static int noOfTriangles(int n)
{
return (n * (n + 2) * (2 * n + 1) / 8);
}
public static void main(String args[])
{
int n = 3;
System.out.print(noOfTriangles(n));
}
}
|
Python3
def noOfTriangles(n):
return n * (n + 2) * (2 * n + 1) // 8
n = 3
print(noOfTriangles(n))
|
C#
using System;
class GFG {
public static int noOfTriangles(int n)
{
return (n * (n + 2) * (2 * n + 1) / 8);
}
public static void Main(String[] args)
{
int n = 3;
Console.Write(noOfTriangles(n));
}
}
|
Javascript
<script>
function noOfTriangles(n)
{
return Math.floor(n * (n + 2)
* (2 * n + 1) / 8);
}
var n = 3;
document.write(noOfTriangles(n));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...