Count subsequences having odd Bitwise OR values in an array
Last Updated :
11 Feb, 2022
Given an array arr[] consisting of N positive integers, the task is to find the number of subsequences from the given array whose Bitwise OR value is odd.
Examples:
Input: arr = [2, 4, 1]
Output: 4
Explanation: Subsequences with odd Bitwise OR values are {1}, {2, 1}, {4, 1}, {2, 4, 1}
Input: arr = [1, 3, 4]
Output: 6
Naive Approach: The simplest approach to solve the problem is to generate all the subsequences of the given array and for each subsequence, check if its Bitwise OR value is odd or not. If it is odd, then increase the count by one. After checking for all subsequences, print the count obtained.
Time Complexity: 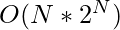
Auxiliary Space: 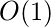
Efficient Approach: Given problem can be solved by observing that for a subsequence to have an odd Bitwise OR value at least one element of the subsequence should be odd. Therefore at least one element in the subsequence should have the least significant digit equal to 1. Follow the steps below to solve this problem:
- Store the count of even and odd elements present in the array arr[] in even and odd variables respectively.
- Traverse the array A[] using the variable i
- If the value of A[i] is odd, increase the value of odd by 1.
- Otherwise, increase the value of even by 1.
- Total combinations with at least one odd element and any number of even elements can be given by: [2^(odd elements) – 1] * 2^(even elements). Since at least one odd element is needed so empty set of combinations of 1 is excluded
Below is the implementation of the approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countSubsequences(vector<int> arr)
{
int odd = 0;
int even = 0;
for (int x : arr) {
if (x & 1)
odd++;
else
even++;
}
return ((1 << odd) - 1) *
(1 << even);
}
int main()
{
vector<int> arr = {2, 4, 1};
cout << countSubsequences(arr);
}
|
Java
import java.io.*;
class GFG {
static int countSubsequences(int arr[])
{
int odd = 0;
int even = 0;
for (int i = 0; i < arr.length; i++) {
if ((arr[i] & 1) != 0)
odd++;
else
even++;
}
return ((1 << odd) - 1) *
(1 << even);
}
public static void main (String[] args) {
int arr[] = {2, 4, 1};
System.out.println(countSubsequences(arr));
}
}
|
Python3
def countSubsequences(arr) :
odd = 0;
even = 0;
for x in arr:
if (x & 1) :
odd += 1;
else :
even += 1;
return ((1 << odd) - 1) * (1 << even);
if __name__ == "__main__" :
arr = [2, 4, 1];
print(countSubsequences(arr));
|
C#
using System;
class GFG {
static int countSubsequences(int []arr)
{
int odd = 0;
int even = 0;
for (int i = 0; i < arr.Length; i++) {
if ((arr[i] & 1) != 0)
odd++;
else
even++;
}
return ((1 << odd) - 1) *
(1 << even);
}
public static void Main (String[] args) {
int []arr = {2, 4, 1};
Console.Write(countSubsequences(arr));
}
}
|
Javascript
<script>
function countSubsequences( arr)
{
let odd = 0;
let even = 0;
for (let x of arr) {
if (x & 1)
odd++;
else
even++;
}
return ((1 << odd) - 1) *
(1 << even);
}
let arr = [2, 4, 1];
document.write(countSubsequences(arr));
</script>
|
Time Complexity: 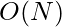
Auxiliary Space: 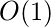
Share your thoughts in the comments
Please Login to comment...