Count subarrays with same even and odd elements
Last Updated :
20 Jan, 2023
Given an array of N integers, count number of even-odd subarrays. An even – odd subarray is a subarray that contains the same number of even as well as odd integers.
Examples :
Input : arr[] = {2, 5, 7, 8}
Output : 3
Explanation : There are total 3 even-odd subarrays.
1) {2, 5}
2) {7, 8}
3) {2, 5, 7, 8}
Input : arr[] = {3, 4, 6, 8, 1, 10}
Output : 3
Explanation : In this case, 3 even-odd subarrays are:
1) {3, 4}
2) {8, 1}
3) {1, 10}
This problem is mainly a variation of count subarrays with equal number of 0s and 1s.
A naive approach would be to check for all possible subarrays using two loops, whether they are even-odd subarrays or not. This approach will take 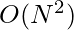 time.
time.
An Efficient approach solves the problem in O(N) time and it is based on following ideas:
- Even-odd subarrays will always be of even length.
- Maintaining track of the difference between the frequency of even and odd integers.
- Hashing of this difference of frequencies is useful in finding number of even-odd subarrays.
The basic idea is to use the difference between the frequency of odd and even numbers to obtain an optimal solution.
We will maintain two integer hash arrays for the positive and negative value of the difference.
-> Example to understand in better way :
-> Consider difference = freq(odd) - freq(even)
-> To calculate this difference, increment the value of 'difference' when there is
an odd integer and decrement it when there is an even integer. (initially, difference = 0)
arr[] = {3, 4, 6, 8, 1, 10}
index 0 1 2 3 4 5 6
array 3 4 6 8 1 10
difference 0 1 0 -1 -2 -1 -2
-> Observe that whenever a value 'k' repeats in the 'difference' array, there exists an
even-odd subarray for each previous occurrence of that value i.e. subarray exists from
index i + 1 to j where difference[i] = k and difference[j] = k.
-> Value '0' is repeated in 'difference' array at index 2 and hence subarray exists for
(0, 2] indexes. Similarly, for repetition of values '-1' (at indexes 3 and 5) and '-2' (at
indexes 4 and 6), subarray exists for (3, 5] and (4, 6] indexes.
Below is the implementation of the O(N) solution described above.
C++
#include <bits/stdc++.h>
using namespace std;
int countSubarrays(int arr[], int n)
{
int difference = 0;
int ans = 0;
int hash_positive[n + 1], hash_negative[n + 1];
fill_n(hash_positive, n + 1, 0);
fill_n(hash_negative, n + 1, 0);
hash_positive[0] = 1;
for (int i = 0; i < n ; i++)
{
if (arr[i] & 1 == 1)
difference++;
else
difference--;
if (difference < 0)
{
ans += hash_negative[-difference];
hash_negative[-difference]++;
}
else
{
ans += hash_positive[difference];
hash_positive[difference]++;
}
}
return ans;
}
int main()
{
int arr[] = {3, 4, 6, 8, 1, 10, 5, 7};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Total Number of Even-Odd subarrays"
" are " << countSubarrays(arr,n);
return 0;
}
|
C
#include <stdio.h>
int countSubarrays(int arr[], int n)
{
int difference = 0;
int ans = 0;
int hash_positive[n + 1], hash_negative[n + 1];
for (int i = 0; i < n + 1; i++)
hash_positive[i] = 0;
for (int i = 0; i < n + 1; i++)
hash_negative[i] = 0;
hash_positive[0] = 1;
for (int i = 0; i < n; i++) {
if (arr[i] & 1 == 1)
difference++;
else
difference--;
if (difference < 0) {
ans += hash_negative[-difference];
hash_negative[-difference]++;
}
else {
ans += hash_positive[difference];
hash_positive[difference]++;
}
}
return ans;
}
int main()
{
int arr[] = { 3, 4, 6, 8, 1, 10, 5, 7 };
int n = sizeof(arr) / sizeof(arr[0]);
printf("Total Number of Even-Odd subarrays are %d ",
countSubarrays(arr, n));
return 0;
}
|
Java
class GFG {
static int countSubarrays(int[] arr, int n)
{
int difference = 0;
int ans = 0;
int[] hash_positive = new int[n + 1];
int[] hash_negative = new int[n + 1];
hash_positive[0] = 1;
for (int i = 0; i < n; i++) {
if ((arr[i] & 1) == 1)
difference++;
else
difference--;
if (difference < 0) {
ans += hash_negative[-difference];
hash_negative[-difference]++;
}
else {
ans += hash_positive[difference];
hash_positive[difference]++;
}
}
return ans;
}
public static void main(String[] args)
{
int[] arr = new int[] { 3, 4, 6, 8, 1, 10, 5, 7 };
int n = arr.length;
System.out.println(
"Total Number of Even-Odd subarrays are "
+ countSubarrays(arr, n));
}
}
|
Python3
def countSubarrays(arr, n):
difference = 0
ans = 0
hash_positive = [0] * (n + 1)
hash_negative = [0] * (n + 1)
hash_positive[0] = 1
for i in range(n):
if (arr[i] & 1 == 1):
difference = difference + 1
else:
difference = difference - 1
if (difference < 0):
ans += hash_negative[-difference]
hash_negative[-difference] = hash_negative[-difference] + 1
else:
ans += hash_positive[difference]
hash_positive[difference] = hash_positive[difference] + 1
return ans
arr = [3, 4, 6, 8, 1, 10, 5, 7]
n = len(arr)
print("Total Number of Even-Odd subarrays are " +
str(countSubarrays(arr, n)))
|
C#
using System;
class GFG
{
static int countSubarrays(int []arr,
int n)
{
int difference = 0;
int ans = 0;
int []hash_positive = new int[n + 1];
int []hash_negative = new int[n + 1];
Array.Clear(hash_positive, 0, n + 1);
Array.Clear(hash_negative, 0, n + 1);
hash_positive[0] = 1;
for (int i = 0; i < n ; i++)
{
if ((arr[i] & 1) == 1)
difference++;
else
difference--;
if (difference < 0)
{
ans += hash_negative[-difference];
hash_negative[-difference]++;
}
else
{
ans += hash_positive[difference];
hash_positive[difference]++;
}
}
return ans;
}
static void Main()
{
int []arr = new int[]{3, 4, 6, 8,
1, 10, 5, 7};
int n = arr.Length;
Console.Write("Total Number of Even-Odd" +
" subarrays are " +
countSubarrays(arr,n));
}
}
|
PHP
<?php
function countSubarrays(&$arr, $n)
{
$difference = 0;
$ans = 0;
$hash_positive = array_fill(0, $n + 1, NULL);
$hash_negative = array_fill(0, $n + 1, NULL);
$hash_positive[0] = 1;
for ($i = 0; $i < $n ; $i++)
{
if ($arr[$i] & 1 == 1)
$difference++;
else
$difference--;
if ($difference < 0)
{
$ans += $hash_negative[-$difference];
$hash_negative[-$difference]++;
}
else
{
$ans += $hash_positive[$difference];
$hash_positive[$difference]++;
}
}
return $ans;
}
$arr = array(3, 4, 6, 8, 1, 10, 5, 7);
$n = sizeof($arr);
echo "Total Number of Even-Odd subarrays".
" are " . countSubarrays($arr, $n);
?>
|
Javascript
<script>
function countSubarrays(arr, n)
{
let difference = 0;
let ans = 0;
let hash_positive = new Array(n + 1);
let hash_negative = new Array(n + 1);
for(let i=0;i<n+1;i++)
{
hash_positive[i] = 0;
hash_negative[i] = 0;
}
hash_positive[0] = 1;
for (let i = 0; i < n; i++)
{
if ((arr[i] & 1) == 1)
{
difference++;
}
else
{
difference--;
}
if (difference < 0)
{
ans += hash_negative[-difference];
hash_negative[-difference]++;
}
else
{
ans += hash_positive[difference];
hash_positive[difference]++;
}
}
return ans;
}
let arr = [3, 4, 6, 8,
1, 10, 5, 7];
let n = arr.length;
document.write("Total Number of Even-Odd"
+ " subarrays are "
+ countSubarrays(arr, n));
</script>
|
OutputTotal Number of Even-Odd subarrays are 7
Complexity Analysis:
- Time Complexity: O(N), where N is the number of integers.
- Auxiliary Space: O(2N), where N is the number of integers.
Another approach:- This approach is much simpler and easy to understand. It can be solved easily by using the same concept of
Count subarrays with equal numbers of 1’s and 0’s. Change the odd elements to -1 and even elements to 1. And now count the ways to find sum=0;
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
long long int countSubarrays(int arr[], int n)
{
long long int k = 0, currsum = 0, count = 0;
unordered_map<int, int> map;
for (int i = 0; i < n; i++) {
if (arr[i] % 2 == 0)
arr[i] = 1;
else if (arr[i] % 2 != 0)
arr[i] = -1;
currsum += arr[i];
if (currsum == k)
count++;
if (map.find(currsum - k) != map.end()) {
count += map[currsum - k];
}
map[currsum]++;
}
return count;
}
int main()
{
int arr[] = { 3, 4, 6, 8, 1, 10, 5, 7 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Total Number of Even-Odd subarrays"
" are "
<< countSubarrays(arr, n);
}
|
Java
import java.util.*;
class GFG {
static long countSubarrays(int arr[], int n)
{
long k = 0, currsum = 0, count = 0;
HashMap<Long, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
if (arr[i] % 2 == 0)
arr[i] = 1;
else if (arr[i] % 2 != 0)
arr[i] = -1;
currsum += arr[i];
if (currsum == k)
count++;
if (map.containsKey(currsum - k)) {
count += map.get(currsum - k);
}
map.put(currsum,map.getOrDefault(currsum,0)+1);
}
return count;
}
public static void main (String[] args) {
int arr[] = { 3, 4, 6, 8, 1, 10, 5, 7 };
int n = arr.length;
System.out.println("Total Number of Even-Odd subarrays are " + countSubarrays(arr, n));
}
}
|
Python3
def countSubarrays(arr, n):
k = 0
currsum = 0
count = 0
map = {}
for i in range(n):
if arr[i] % 2 == 0:
arr[i] = 1
else:
arr[i] = -1
currsum += arr[i]
if currsum == k:
count += 1
if currsum - k in map:
count += map[currsum - k]
if currsum not in map:
map[currsum] = 1
else:
map[currsum] += 1
return count
arr = [3, 4, 6, 8, 1, 10, 5, 7]
n = len(arr)
print("Total Number of Even-Odd subarrays are", countSubarrays(arr, n))
|
C#
using System;
using System.Collections.Generic;
using System.Collections;
public class GFG
{
public static long countSubarrays(int[] arr, int n)
{
var k = 0;
var currsum = 0;
var count = 0;
var map = new Dictionary<long, int>();
for (int i = 0; i < n; i++)
{
if (arr[i] % 2 == 0)
{
arr[i] = 1;
}
else if (arr[i] % 2 != 0)
{
arr[i] = -1;
}
currsum += arr[i];
if (currsum == k)
{
count++;
}
if (map.ContainsKey(currsum - k))
{
count += map[currsum - k];
}
map[currsum] = (map.ContainsKey(currsum) ? map[currsum] : 0) + 1;
}
return count;
}
public static void Main(String[] args)
{
int[] arr = {3, 4, 6, 8, 1, 10, 5, 7};
var n = arr.Length;
Console.WriteLine("Total Number of Even-Odd subarrays are " + GFG.countSubarrays(arr, n).ToString());
}
}
|
Javascript
function countSubarrays(arr, n){
var k = 0, currsum = 0, count = 0;
var map = new Map();
for(let i=0;i<n;i++){
if(arr[i]%2==0){
arr[i] = 1;
}
else if(arr[i]%2!=0){
arr[i] = -1;
}
currsum += arr[i];
if(currsum == k){
count++;
}
if(map.has(currsum-k)){
count += map.get(currsum-k);
}
var temp = (map.has(currsum) ? map.get(currsum) : 0) + 1;
map.set(currsum, temp);
}
return count;
}
var arr = [ 3, 4, 6, 8, 1, 10, 5, 7 ];
var n = arr.length;
console.log("Total Number of Even-Odd subarrays are " + countSubarrays(arr, n));
|
OutputTotal Number of Even-Odd subarrays are 7
Complexity Analysis:
- Time Complexity: O(N).
- Auxiliary Space: O(N).
Share your thoughts in the comments
Please Login to comment...