Count pairs of similar rectangles possible from a given array

Given a 2D array A[][2] of size N (1 ≤ N ≤ 10³), where A[i][0] and A[i][1] denotes the length and breadth of rectangle i respectively.

Two rectangle i and j where (i < j) are similar if the ratio of their length and breadth is equal

A[i][0] / A[i][1] = A[j][0] / A[j][1]

The task is to count the pair of rectangles that are nearly similar. 

Examples:

Input : A[][2] = {{4, 8}, {15, 30}, {3, 6}, {10, 20}}
Output: 6
Explanation: Pairs of similar rectangles are (0, 1), {0, 2), (0, 3), (1, 2), (1, 3), (2, 3). For every rectangle, ratio of length : breadth is 1 : 2

Input : A[][2] = {{2, 3}, {4, 5}, {7, 8}}
Output: 0
Explanation: No pair of similar rectangles exists.

Method 1 (Simple Comparison Method)

Approach: Follow the steps to solve the problem 

• Traverse the array.
• For every pair such that (i < j), check whether the rectangles are similar or not by checking if the condition A[i][0] / A[i][1] = A[j][0] / A[j][1] is satisfied or not.
• If found to be true, increment the count.
• Finally, print the count obtained.

Below is the implementation of the above approach: 

C++

// C++ Program for the above approach

#include <iostream>
using namespace std;

// Function to calculate the count
// of similar rectangles
int getCount(int rows,
             int columns, int A[][2])
{
    int res = 0;

    for (int i = 0; i < rows; i++) {
        for (int j = i + 1; j < rows; j++) {

            if (A[i][0] * 1LL * A[j][1]
                == A[i][1] * 1LL * A[j][0]) {

                res++;
            }
        }
    }
    return res;
}

// Driver Code
int main()
{
    // Input
    int A[][2]
        = { { 4, 8 }, { 10, 20 }, { 15, 30 }, { 3, 6 } };
    int columns = 2;
    int rows = sizeof(A) / sizeof(A[0]);

    cout << getCount(rows, columns, A);

    return 0;
}

Java

// Java program for the above approach
import java.util.*;
class GFG{

// Function to calculate the count
// of similar rectangles
static int getCount(int rows, int columns,
                    int[][] A)
{
    int res = 0;
    for(int i = 0; i < rows; i++)
    {
        for(int j = i + 1; j < rows; j++)
        {
            if (A[i][0] * A[j][1] ==
                A[i][1] * A[j][0])
            {
                res++;
            }
        }
    }
    return res;
}

// Driver Code
public static void main(String[] args)
{

    // Input
    int[][] A = { { 4, 8 }, { 10, 20 },
                 { 15, 30 }, { 3, 6 } };
    int columns = 2;
    int rows = 4;

    System.out.print(getCount(rows, columns, A));
}
}

// This code is contributed by code_hunt.

Python3

# Python3 program for the above approach

# Function to calculate the count
# of similar rectangles
def getCount(rows, columns, A):

    res = 0

    for i in range(rows):
        for j in range(i + 1, rows, 1):
            if (A[i][0] * A[j][1] ==
                A[i][1] * A[j][0]):
                res += 1

    return res

# Driver Code
if __name__ == '__main__':

    # Input
    A =  [ [ 4, 8 ], [ 10, 20 ],
           [ 15, 30 ], [ 3, 6 ] ]
    columns = 2
    rows =  len(A)

    print(getCount(rows, columns, A))

# This code is contributed by SURENDRA_GANGWAR

C#

// C# program for the above approach
using System;

class GFG{

// Function to calculate the count
// of similar rectangles
static int getCount(int rows, int columns,
                    int[,] A)
{
    int res = 0;

    for(int i = 0; i < rows; i++)
    {
        for(int j = i + 1; j < rows; j++)
        {
            if (A[i, 0] * A[j, 1] ==
                A[i, 1] * A[j, 0])
            {
                res++;
            }
        }
    }
    return res;
}

// Driver code
static void Main()
{

    // Input
    int[,] A = { { 4, 8 }, { 10, 20 },
                 { 15, 30 }, { 3, 6 } };
    int columns = 2;
    int rows = 4;

    Console.Write(getCount(rows, columns, A));
}
}

// This code is contributed by divyesh072019

Javascript

<script>

// Javascript program for the above approach

// Function to calculate the count
// of similar rectangles
function getCount(rows, columns, A)
{
    var res = 0;
    for(var i = 0; i < rows; i++)
    {
        for(var j = i + 1; j < rows; j++)
        {
            if (A[i][0] * A[j][1] ==
                A[i][1] * A[j][0])
            {
                res++;
            }
        }
    }
    return res;
}

// Driver Code

// Input
var A = [ [ 4, 8 ], [ 10, 20 ],
          [ 15, 30 ], [ 3, 6 ] ];
var columns = 2;
var rows = 4;

document.write(getCount(rows, columns, A));

// This code is contributed by kirti

</script>

Output

6

Time Complexity: O(N²)
Auxiliary Space: O(1)

Method 2 (Using HashMap)

Instead of comparing one rectangle’s ratio to another rectangle’s directly, we can store all the calculated ratios in the HashMap. Since HashMap has the access cost of O(1), that would allow a fast lookup for other rectangles with the same ratio and store them together. The number of pairs of similar rectangles can be derived from the number of rectangles with the same ratio using \frac{N \times (N – 1)}{2}. The reason one can use the mentioned equation to find the number of pairs of similar rectangles is that the number of pairs increases by 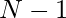 each time a rectangle with the same ratio is added.

C++

// C++ Program for the hashmap Approach
#include <iostream>
#include <unordered_map>
using namespace std;

// Get the count of all pairs of similar rectangles

int getCount(int rows, int columns, int sides[][2])
{
    // Initialize the result value and
    // map to store the ratio to the rectangles
    int ans = 0;
    unordered_map<double, int> umap;

    // Calculate the rectangular ratio and save them
    for (int i = 0; i < rows; i++)
    {
        double ratio = (double)sides[i][0] / sides[i][1];
        umap[ratio]++;
    }

    // Calculate pairs of similar rectangles from its common ratio
    for (auto x : umap)
    {
        int value = x.second;
        if (value > 1)
        {
            ans += (value * (value - 1)) / 2;
        }
    }
    return ans;
}

int main()
{
    int sides[4][2] = {{4, 8}, {10, 20}, {15, 30}, {3, 6}};
    int rows = 4;
    int columns = 2;
    cout << getCount(rows, columns, sides);
    return 0;

    //this code is contributed by krishna_6431
}

Java

import java.util.*;

class GFG {

      // Get the count of all pairs of similar rectangles
    public static int getCount(int rows, int columns,
                                int[][] sides)
    {
          // Initialize the result value and
          // map to store the ratio to the rectangles
        int res = 0;
        Map<Double, Integer> ratio
            = new HashMap<Double, Integer>();

          // Calculate the rectangular ratio and save them
          for (int i = 0; i < rows; i++) {
            double rectRatio = (double) sides[i][0] /
                  sides[i][1];
              if (ratio.get(rectRatio) == null) {
                  ratio.put(rectRatio, 0);
            }
              ratio.put(rectRatio, ratio.get(rectRatio) + 1);
        }

          // Calculate pairs of similar rectangles from
          // its common ratio
        for (double key : ratio.keySet()) {
            int val = ratio.get(key);
            if (val > 1) {
                res += (val * (val - 1)) / 2;
            }
        }

        return res;
    }

      public static void main(String[] args) {
          int[][] A = {{4, 8}, {10, 20}, {15, 30}, {3, 6}};
          int columns = 2;
          int rows = 4;

          System.out.println(getCount(rows, columns, A));
    }
}

// This code is contributed by nathnet

Python3

# Python 3 Program for the hashmap Approach
from collections import defaultdict

# Get the count of all pairs of similar rectangles
def getCount(rows,  columns, sides):

    # Initialize the result value and
    # map to store the ratio to the rectangles
    ans = 0
    umap = defaultdict(int)

    # Calculate the rectangular ratio and save them
    for i in range(rows):

        ratio = sides[i][0] / sides[i][1]
        umap[ratio] += 1

    # Calculate pairs of similar rectangles from its common ratio
    for x in umap:

        value = umap[x]
        if (value > 1):
            ans += (value * (value - 1)) / 2

    return ans

# Driver code
if __name__ == "__main__":

    sides = [[4, 8], [10, 20], [15, 30], [3, 6]]
    rows = 4
    columns = 2
    print(int(getCount(rows, columns, sides)))

    # This code is contributed by ukasp.

C#

using System;
using System.Collections.Generic;

class GFG {

    // Get the count of all pairs of similar rectangles
    public static int getCount(int rows, int columns,
                               int[, ] sides)
    {
        // Initialize the result value and
        // map to store the ratio to the rectangles
        int res = 0;
        Dictionary<double, int> ratio
            = new Dictionary<double, int>();

        // Calculate the rectangular ratio and save them
        for (int i = 0; i < rows; i++) {
            double rectRatio
                = (double)sides[i, 0] / sides[i, 1];
            if (!ratio.ContainsKey(rectRatio)) {
                ratio[rectRatio] = 0;
            }
            ratio[rectRatio] = ratio[rectRatio] + 1;
        }

        // Calculate pairs of similar rectangles from
        // its common ratio
        foreach(KeyValuePair<double, int> p in ratio)
        {
            int val = p.Value;
            if (val > 1) {
                res += (val * (val - 1)) / 2;
            }
        }

        return res;
    }

  // Driver code
    public static void Main(string[] args)
    {
        int[, ] A = {
            { 4, 8 }, { 10, 20 }, { 15, 30 }, { 3, 6 }
        };
        int columns = 2;
        int rows = 4;

        Console.WriteLine(getCount(rows, columns, A));
    }
}

// This code is contributed by ukasp.

Javascript

<script>

// JavaScript Program for the hashmap Approach

// Get the count of all pairs of similar rectangles
function getCount(rows, columns, sides)
{
    // Initialize the result value and
    // map to store the ratio to the rectangles
    let ans = 0;
    let umap = new Map();

    // Calculate the rectangular ratio and save them
    for (let i = 0; i < rows; i++)
    {
        let ratio = sides[i][0] / sides[i][1];
        if(umap.has(ratio)){
             umap.set(ratio,umap.get(ratio)+1);
        }
        else umap.set(ratio,1);
    }

    // Calculate pairs of similar rectangles from its common ratio
    for (let [x,y] of umap)
    {
        let value = y;
        if (value > 1)
        {
            ans += (value * (value - 1)) / 2;
        }
    }
    return ans;
}

// driver code
let sides = [[4, 8], [10, 20], [15, 30], [3, 6]];
let rows = 4;
let columns = 2;
document.write(getCount(rows, columns, sides));

// This code is contributed by shinjanpatra

</script>

Output

6

Time Complexity: O(N)

Auxiliary Space: O(N)