Count of ways to represent N as sum of a prime number and twice of a square

Difficulty Level : Easy
Last Updated : 06 Jun, 2021

Given an integer N, the task is to count the number of ways so that N can be written as the sum of a prime number and twice of a square, i.e.

$N = 2*A^{2} + P$

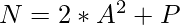
, where P can be any prime number and A is any positive integer.
Note:

$N <= 10^{6}$

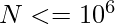
Examples:

Input: N = 9
Output: 1
Explanation:
9 can be represented as sum of prime number and twice a square in only one way –
$N = 9 = 7 + 2*(1^{2})$

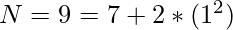
Input: N = 15
Output: 2
Explanation:
15 can be represented as sum of prime number and twice a square in two ways –
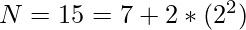$N = 15 = 7 + 2 * (2^{2})$ [Tex]N = 15 = 13 + 2 * (1^{2}) [/Tex]

Approach: The idea is to use Sieve of Eratosthenes to find all the primes and then for each prime number check for every possible number starting from 1. If any prime number and twice a square is equal to the given number then increment the count of the number of ways by 1.
Below is the implementation of the above approach:

C++

// C++ implementation to count the
// number of ways a number can be
// written as sum of prime number
// and twice a square
 
#include <bits/stdc++.h>
 
using namespace std;
long long int n = 500000 - 2;
vector<long long int> v;
 
// Function to mark all the
// prime numbers using sieve
void sieveoferanthones()
{
    bool prime[n + 1];
 
    // Intially all the numbers
    // are marked as prime
    memset(prime, true,
           sizeof(prime));
 
    // Loop to mark the prime numbers
    // upto the Square root of N
    for (long long int i = 2; i <= sqrt(n);
         i++) {
        if (prime[i])
            for (long long int j = i * i;
                 j <= n; j += i) {
                prime[j] = false;
            }
    }
 
    // Loop to store the prime
    // numbers in an array
    for (long long int i = 2; i < n; i++) {
        if (prime[i])
            v.push_back(i);
    }
}
 
// Function to find the number
// ways to represent a number
// as the sum of prime number and
// square of a number
void numberOfWays(long long int n)
{
    long long int count = 0;
 
    // Loop to iterate over all the
    // possible prime numbers
    for (long long int j = 1;
         2 * (pow(j, 2)) < n; j++) {
        for (long long int i = 1;
             v[i] + 2 <= n; i++) {
 
            // Increment the count if
            // the given number is a
            // valid number
            if (n == v[i]
+ (2 * (pow(j, 2))))
                count++;
        }
    }
    cout << count << endl;
}
 
// Driver Code
int main()
{
    sieveoferanthones();
    long long int n = 9;
 
    // Function Call
    numberOfWays(n);
    return 0;
}

Java

// Java implementation to count the
// number of ways a number can be
// written as sum of prime number
// and twice a square
import java.util.*;
class GFG{
 
static int n = 500000 - 2;
static Vector<Integer> v =
              new Vector<>();
 
// Function to mark all the
// prime numbers using sieve
static void sieveoferanthones()
{
  boolean []prime = new boolean[n + 1];
 
  // Intially all the numbers
  // are marked as prime
  Arrays.fill(prime, true);
 
  // Loop to mark the prime numbers
  // upto the Square root of N
  for (int i = 2;
           i <= Math.sqrt(n); i++)
  {
    if (prime[i])
      for (int j = i * i;
               j <= n; j += i)
      {
        prime[j] = false;
      }
  }
 
  // Loop to store the prime
  // numbers in an array
  for (int i = 2; i < n; i++)
  {
    if (prime[i])
      v.add(i);
  }
}
 
// Function to find the number
// ways to represent a number
// as the sum of prime number and
// square of a number
static void numberOfWays(int n)
{
  int count = 0;
 
  // Loop to iterate over all the
  // possible prime numbers
  for (int j = 1; 2 *
      (Math.pow(j, 2)) < n; j++)
  {
    for (int i = 1; v.get(i) +
             2 <= n; i++)
    {
      // Increment the count if
      // the given number is a
      // valid number
      if (n == v.get(i) +
         (2 * (Math.pow(j, 2))))
        count++;
    }
  }
  System.out.print(count + "\n");
}
 
// Driver Code
public static void main(String[] args)
{
  sieveoferanthones();
  int n = 9;
 
  // Function Call
  numberOfWays(n);
}
}
 
// This code is contributed by Princi Singh

Python3

# Python3 implementation to count the
# number of ways a number can be
# written as sum of prime number
# and twice a square
import math
 
n = 500000 - 2
v = []
 
# Function to mark all the
# prime numbers using sieve
def sieveoferanthones():
     
    prime = [1] * (n + 1)
 
    # Loop to mark the prime numbers
    # upto the Square root of N
    for i in range(2, int(math.sqrt(n)) + 1):
        if (prime[i] != 0):
             
            for j in range(i * i, n + 1, i):
                prime[j] = False
             
    # Loop to store the prime
    # numbers in an array
    for i in range(2, n):
        if (prime[i] != 0):
            v.append(i)
     
# Function to find the number
# ways to represent a number
# as the sum of prime number and
# square of a number
def numberOfWays(n):
     
    count = 0
 
    # Loop to iterate over all the
    # possible prime numbers
    j = 1
    while (2 * (pow(j, 2)) < n):
        i = 1
        while (v[i] + 2 <= n):
 
            # Increment the count if
            # the given number is a
            # valid number
            if (n == v[i] +
               (2 * (math.pow(j, 2)))):
                count += 1
                 
            i += 1
             
        j += 1
         
    print(count)
 
# Driver Code
sieveoferanthones()
n = 9
 
# Function call
numberOfWays(n)
 
# This code is contributed by sanjoy_62

C#

// C# implementation to count the
// number of ways a number can be
// written as sum of prime number
// and twice a square        
using System;
using System.Collections;
using System.Collections.Generic;
 
class GFG{        
             
static int n = 500000 - 2;
 
static ArrayList v = new ArrayList();
 
// Function to mark all the
// prime numbers using sieve
static void sieveoferanthones()
{
    bool []prime = new bool[n + 1];
 
    // Intially all the numbers
    // are marked as prime
    Array.Fill(prime, true);
 
    // Loop to mark the prime numbers
    // upto the Square root of N
    for(int i = 2;
            i <= (int)Math.Sqrt(n); i++)
    {
        if (prime[i])
        {
            for(int j = i * i;
                    j <= n; j += i)
            {
                prime[j] = false;
            }
        }
    }
 
    // Loop to store the prime
    // numbers in an array
    for(int i = 2; i < n; i++)
    {
        if (prime[i])
            v.Add(i);
    }
}
 
// Function to find the number
// ways to represent a number
// as the sum of prime number and
// square of a number
static void numberOfWays(int n)
{
    int count = 0;
 
    // Loop to iterate over all the
    // possible prime numbers
    for(int j = 1;
            2 * (Math.Pow(j, 2)) < n; j++)
    {
        for(int i = 1;
           (int)v[i] + 2 <= n; i++)
        {
             
            // Increment the count if
            // the given number is a
            // valid number
            if (n == (int)v[i] +
                     (2 * (Math.Pow(j, 2))))
                count++;
        }
    }
    Console.Write(count);
}        
         
// Driver Code        
public static void Main (string[] args)
{        
    sieveoferanthones();
    int n = 9;
 
    // Function call
    numberOfWays(n);
}        
}
 
// This code is contributed by rutvik_56

Javascript

<script>
 
// JavaScript implementation to count the
// number of ways a number can be
// written as sum of prime number
// and twice a square
 
let n = 500000 - 2;
let v = [];
  
// Function to mark all the
// prime numbers using sieve
function sieveoferanthones()
{
  let prime = Array.from({length: n+1},
                          (_, i) => true);
  
  // Loop to mark the prime numbers
  // upto the Square root of N
  for (let i = 2;
           i <= Math.sqrt(n); i++)
  {
    if (prime[i])
      for (let j = i * i;
               j <= n; j += i)
      {
        prime[j] = false;
      }
  }
  
  // Loop to store the prime
  // numbers in an array
  for (let i = 2; i < n; i++)
  {
    if (prime[i])
      v.push(i);
  }
}
  
// Function to find the number
// ways to represent a number
// as the sum of prime number and
// square of a number
function numberOfWays(n)
{
  let count = 0;
  
  // Loop to iterate over all the
  // possible prime numbers
  for (let j = 1; 2 *
      (Math.pow(j, 2)) < n; j++)
  {
    for (let i = 1; v[i] +
             2 <= n; i++)
    {
      // Increment the count if
      // the given number is a
      // valid number
      if (n == v[i] +
         (2 * (Math.pow(j, 2))))
        count++;
    }
  }
  document.write(count + "<br/>");
}
  
  // Driver Code
     
    sieveoferanthones();
  let N = 9;
  
  // Function Call
  numberOfWays(N);
                  
</script>

Output:

Attention reader! Don’t stop learning now. Get hold of all the important mathematical concepts for competitive programming with the Essential Maths for CP Course at a student-friendly price. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

My Personal Notes

Related Articles

Count of ways to represent N as sum of a prime number and twice of a square

C++

Java

Python3

C#

Javascript