Count non decreasing subarrays of size N from N Natural numbers
Last Updated :
03 Feb, 2022
Given are N natural numbers, the task is to find the count of the subarrays of size N that can be formed using elements from 1 to N such that each element in the subarray is smaller than or equal to the elements to its right (a[i] ? a[i+1]).
Examples:
Input: N = 2
Output: 3
Explanation:
Given array of N natural numbers: {1, 2}
Required subarrays that can be formed: [1, 1], [1, 2], [2, 2].
Input: N = 3
Output: 10
Explanation:
Given array of N natural numbers: {1, 2, 3}
Required subarrays that can be formed: [1, 1, 1], [1, 1, 2], [1, 2, 2], [2, 2, 2], [1, 1, 3], [1, 3, 3], [3, 3, 3], [2, 2, 3], [2, 3, 3], [1, 2, 3].
Approach:
- Since each element of the array is between 1 to N and the subarrays can have duplicate elements in non-descending order, i.e., a[0] ? a[1] ? …. ? a[N – 1].
- The number of ways of choosing r objects with replacement from n objects is
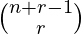 (using Combination with repetition).
(using Combination with repetition). - Here r = N and n = N as we can choose from 1 to N. So the count of all the sorted array of length N with elements from 1 to N will be
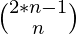 .
. - Now this can be further expanded with the help of Binomial Coefficients. The coefficient obtained from this will be the required subarray’s count.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int binomialCoeff(int n, int k)
{
int C[k + 1];
memset(C, 0, sizeof(C));
C[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = min(i, k); j > 0; j--)
C[j] = C[j] + C[j - 1];
}
return C[k];
}
int count_of_subarrays(int N)
{
int count = binomialCoeff(2 * N - 1, N);
return count;
}
int main()
{
int N = 3;
cout << count_of_subarrays(N) << "\n";
}
|
Java
class GFG
{
static int binomialCoeff(int n, int k)
{
int []C = new int[k + 1];
C[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = Math.min(i, k); j > 0; j--)
C[j] = C[j] + C[j - 1];
}
return C[k];
}
static int count_of_subarrays(int N)
{
int count = binomialCoeff(2 * N - 1, N);
return count;
}
public static void main(String[] args)
{
int N = 3;
System.out.print(count_of_subarrays(N)+ "\n");
}
}
|
Python3
def binomialCoeff(n, k) :
C = [0] * (k + 1);
C[0] = 1;
for i in range(1, n + 1) :
for j in range(min(i, k), 0, -1) :
C[j] = C[j] + C[j - 1];
return C[k];
def count_of_subarrays(N) :
count = binomialCoeff(2 * N - 1, N);
return count;
if __name__ == "__main__" :
N = 3;
print(count_of_subarrays(N)) ;
|
C#
using System;
class GFG
{
static int binomialCoeff(int n, int k)
{
int []C = new int[k + 1];
C[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = Math.Min(i, k); j > 0; j--)
C[j] = C[j] + C[j - 1];
}
return C[k];
}
static int count_of_subarrays(int N)
{
int count = binomialCoeff(2 * N - 1, N);
return count;
}
public static void Main()
{
int N = 3;
Console.WriteLine(count_of_subarrays(N));
}
}
|
Javascript
<script>
function binomialCoeff(n, k)
{
var C = Array(k+1).fill(0);
C[0] = 1;
for (var i = 1; i <= n; i++) {
for (var j = Math.min(i, k); j > 0; j--)
C[j] = C[j] + C[j - 1];
}
return C[k];
}
function count_of_subarrays(N)
{
var count = binomialCoeff(2 * N - 1, N);
return count;
}
var N = 3;
document.write( count_of_subarrays(N));
</script>
|
Time Complexity: O(N2)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...