Continuity of Functions

Continuity of functions is an important unit of Calculus as it forms the base and it helps us further to prove whether a function is differentiable or not. A continuous function is a function which when drawn on a paper does not have a break. The continuity can also be proved using the concept of limits. If a function is continuous then the limit values and the function value at that point should be the same. The curves which do not have continuity at a particular point are said to be discontinuous at that point. All of these will be discussed in detail further, so let’s start our learning about “Continuity of Functions.”

What is Continuity?

A function is said to be continuous at every point if the limit exists at that point and also the value of the function at that point exists. We can prove the continuity of the function using the concept of limits as the limit of any function tell us where the function approaches when input approaches some real number. When the limit of any function and the value of that function is the same, then we say that the function is continuous at that point and if this holds for all the domains for which the function is defined. Thus, the function is continuous.

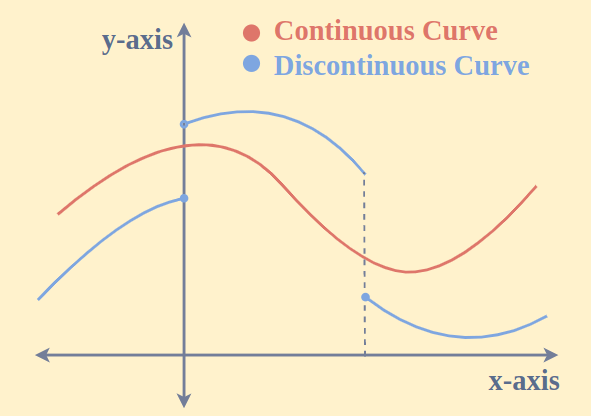
The best example of Continuous functions is Trigonometric functions such as sin(x) and cos(x). They are periodic functions and the values of the functions exist at each point.

One-Sided Continuity

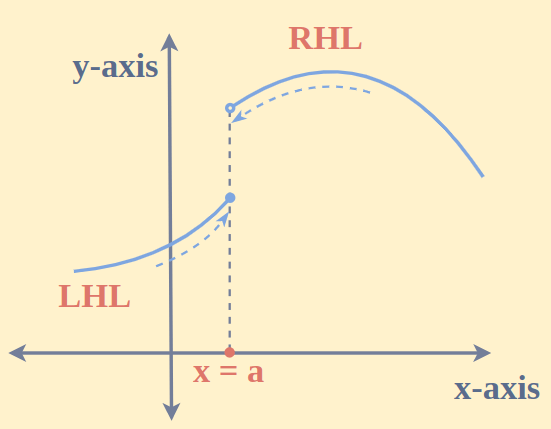
One-Sided Continuity is the continuity in which the input approaches the point either from the left side or right side respectively to the value of the function at that input. We usually use + or – as an exponent on the input. 

For the left side, we use the negative sign and this left side is known as Left Hand Limit abbreviated as LHL. The LHL is denoted by Iim_x→a-f(x). 

For the right side, we use the positive sign. The right side is also known as Right Hand Limit. It is denoted by Iim_x→a+f(x)

Continuity of a Function Definition

Mathematically, a function f(x) is continuous at a point x = a, if the following conditions hold:

• f(a) exists and has a finite value.
• Iim_x→a f(x) exists ( LHL = RHL at x = a)
• Iim_x→a f(x) = f(a) i.e., Iim_x→a- f(x) = f(a) = Iim_x→a+ f(x)

In simpler terms, continuity means that there are no sudden jumps, holes, or breaks in the graph of the function. The function can be traced without lifting the pen from the paper.

Note: The above three conditions are respectively called Function Condition, Limit Condition, and Point Condition.

Read more about Continuity and Discontinuity.

Continuity of Function Examples

Let us check the continuity of the function f(x) = sin (x) at a = 0

Let us find the value of the function at a=0

f(0) = sin(0) = 0

Now calculating the Left-Hand limits and the Right Hand Limits respectively we get

LHL = lim_{x → 0-} f(x)
⇒ LHL = lim_{h → 0} f(0 – h)
⇒ LHL = lim_{h → 0} sin(-h)
⇒ LHL = – lim_{h → 0} sin(h)
⇒ LHL = 0

RHL = lim_{x → 0+} f(x)
⇒ RHL = lim_{h → 0} f(0 + h)
⇒ RHL = lim_{h → 0} sin(h)
⇒ RHL = lim_{h → 0} sin(h)
⇒ RHL = 0

The condition Iim_(x→0-)f(x)=f(0)=Iim_(x→0+)f(x) is satisfied. Hence the function is continuous at x = 0

Note: All Polynomial, logarithmic, and exponential functions such as e^x are continuous in all the domains.

Techniques for Determining Continuity

There are different techniques for determining Continuity. Some of them are as follows:

Algebraic Manipulation

Here we use Algebraic tricks such as factorization, the use of Trigonometric Identities, etc to solve continuity-related problems. Let us elaborate with the help of an example.

Example: Let f(x) be defined as follows

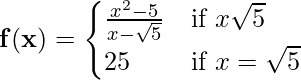
Test the continuity at x = √5.

Solution:

If we put x = √5 in the function (x² – 5) / (x – 5) then the function is undefined. 

Therefore we need to factorize and simplify the function.

lim_x→√5 (x² – 5) / (x – √5)

= lim_x→√5 [(x – √5)(x + √5)]/(x – √5)

= lim_x→√5 (x + √5) = 2√5

And, as at x = √5, function is given by f(x) = f(√5)

Hence the function is continuous.

Piecewise Function

A piecewise function is a function that is defined differently for different functions and is said to be continuous if the graph of the function is continuous at some intervals. Let’s consider an example to understand it better.

Example: Let f(x) be defined as follows.

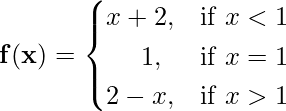
Test the continuity at x = 1.

Solution:

Let us calculate the Left Hand Limit

LHL = lim_{x → 1-} f(x) 
⇒ LHL = lim_{h → 0}  f(1 – h)
⇒ LHL = lim_{h → 0} (1 – h + 2)
⇒ LHL = lim_{h → 0}  (3 – h)
⇒ LHL = 3

f(1) = 1 is given

and,

RHL = lim_{x → 1+} f(x)
⇒ RHL = lim_{h → 0} f(1 + h)
⇒ RHL = lim_{h → 0} (2 – (1 + h))
⇒ RHL = lim_{h → 0} 1
⇒ RHL = 1

The Right Hand Limit is equal to f(1) but is not equal to Left Hand Limit. Hence the function is not continuous.

Rational Functions

Rational functions are of the form p/q where q is not equal to 0. If radicals are present we can check the continuity of these types of functions by multiplying the numerator and denominator with the conjugate of the denominator. The example is as follows:

Example: Let f(x) be defined as follows.

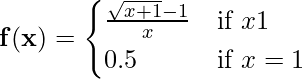
Check the continuity at x = 1.

Solution:

lim_{x → 0} (√(x + 1) – 1) / x

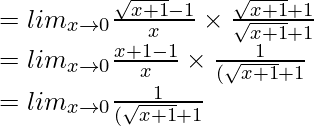
= 1/2 = 0.5

And f(1) = 0.5

Hence it is continuous at x=1.

What is Discontinuity?

If any of the continuity conditions fails, then the function is said to be discontinuous. Alternatively, it can be said that if there occurs a break when a part is drawn on the graph paper in a given interval, then also it defines discontinuity. There are different kinds of Discontinuity.

Jump Discontinuity

This is the discontinuity in which the limit values of the function are different. It means that the Left Hand Limit and the Right Hand Limit exist but the values are different thereby not satisfying the condition Iim_x→a-f(x) = Iim_x→a+f(x)

Let us illustrate with the help of an example

For a function f(x), if 

lim_{x → 3-} f(x) = 3, and

lim_{x → 3+} f(x) = 8

We can see the Left Hand Limit and the Right Hand Limit exists but they are not the same. 

Hence this is a jump discontinuity.

Point Discontinuity

This discontinuity occurs in rational expressions in which both the numerator and the denominator become 0. However, this discontinuity can be removed. Let us illustrate with the help of an example

Example: Check the continuity of the following function f(x) at x = 1,

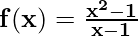
Solution:

This is a point discontinuity since if we put x =1 in the function it is of the form 0/0. However, by factorizing this discontinuity can be removed.

LHL = lim_{x → 1-} f(x)
⇒ LHL = lim_{x → 1-} [(x – 1)(x + 1) / (x – 1)]
⇒ LHL = lim_{x → 1-} (x + 1)
⇒ LHL = lim_{h → 0} (1 – h + 1)
⇒ LHL = 2

and 

RHL = lim_{x → 1+} f(x)
⇒ RHL = lim_{x → 1+} [(x – 1)(x + 1) / (x – 1)]
⇒ RHL = lim_{x → 1+} (x + 1)
⇒ RHL = lim_{h → 0} (1 + h + 1)
⇒ RHL = 2

Hence, it is continuous at x = 1.

Infinite Discontinuity

This discontinuity occurs when either the value of the left-hand limit tends to negative infinity or the value of the right-hand limit tends to infinity. Let us illustrate with the help of an example.

Example: Check the continuity of the following function at x = 0,

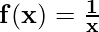
Solution:

LHL = lim_{x → 0-} f(x)
⇒ LHL = lim_{x → 0-} (1 / x)
⇒ LHL = lim_{h → 0} (1 / (0 – h))
⇒ LHL = -∞

and, 

RHL = lim_{x → 0+} f(x)
⇒ RHL = lim_{x → 0+} (1 / x)
⇒ RHL = lim_{h → 0} (1 / (0 + h))
⇒ RHL = +∞

Thus, at x = 0 function has Infinite Discontinuity.

Solved Problems with Continuity

Problem 1: For function f(x) defined as 

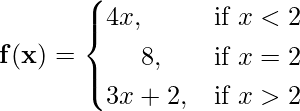
Check the continuity at x =2.

Solution:

We will calculate the limits at x = 2

LHL = Iim_(x→2-) f(x) = Iim_(h→0) f(2-h)

⇒ LHL = Iim_(h→0)4×(2-h)

⇒ LHL = 4×(2-0)

⇒ LHL = 8

RHL = Iim_(x→0+) f(x) = Iim_{(h → 0)} f(0+h)

⇒ RHL = Iim_{(h → 0)}3×(2+h)+2

⇒ RHL = 3×(2+0)+2

⇒ RHL = 8

Problem 2: Find the value of ‘m’ at which the function is continuous at x = 9

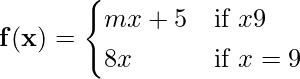
Solution:

lim_{x → 9-} f(x) = lim (h → 0) f(9 – h)
LHL = lim_{h → 0} [m × (9 – h) + 5]
LHL = 9m + 5

RHL = lim_{x → 9+} f(x)
⇒ RHL = lim_{h → 0} f(9 + h)
⇒ RHL = lim_{h → 0} [8 × (9 + h)]
⇒ RHL = 72

For a function to be continuous Left Hand Limit is equal to Right Hand Limit

Thus, 9m + 5 =72

⇒ m = 7.4444

For the function to be continuous the value of m should be 7.44.

Problem 3: Test the continuity at x = 1, for the following function.

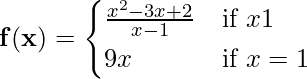
Solution:

If we put x = 1 in the function (x² – 3x + 2) / (x – 1) then the function is undefined. Therefore we need to factorize and simplify the function.

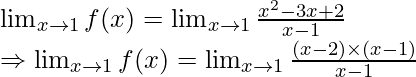
⇒ lim_x→1 f(x) = lim_x→1 (x − 2)
⇒ lim_x→1 f(x) = −1
⇒ lim_x→1 f(x) = f(1)

Hence, the function is continuous at x = 1.

Problem 4: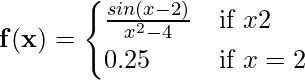 

Test the continuity at x = 2 of the above-mentioned function.

Solution:

If we put x = 2 in the function sin(x – 2) / (x² – 4) then the function is undefined. Therefore we need to factorize and simplify the function.

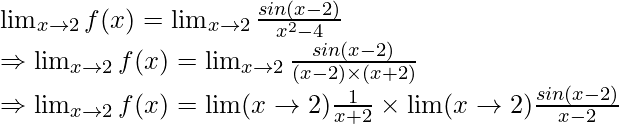
⇒ lim_x→2 ​f(x) = 1/4 = 0.25
⇒ lim_x→2 ​f(x) = f(2) = 0.25

Thus, the function is continuous at x = 2.

Problem 5: Find the relation between m and n if the function is continuous at point x=-5

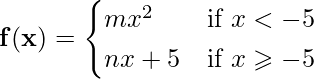
Solution:

We will compute the Left Hand Limit and Right Hand Limit separately

LHL = lim_{x→−5 −} mx²
⇒ LHL = lim_h→0 m×(−5−h)²
⇒LHL = 25m

RHL = lim _{x→−5 +} nx+5 
⇒ RHL = lim_h→0  n×(-5+h)+5 
⇒ RHL = -5n+5

For a function to be continuous LHL = RHL

25m = -5n + 5 
⇒ 25m + 5n = 5
⇒ 5m + n = 1

FAQs on Continuity of Functions

1. Define Continuity.

Continuity of the curve is defined in which the curve can be drawn on a graph paper with a single stroke. Continuity can also be defined when the Left Hand Limit is equal to the Right Hand Limit.

2. What is the Difference between Continuity and Limit?

A limit is used to find the value of a function when the function approaches a particular point. Using Limits one can prove the continuity of the function. A function is said to be continuous when the Left hand limit and the Right Hand lImit are same.

3. What are the Conditions for a Function to be Continuous?

For a function to be continuous at point x=b

• f(b) exists and has a finite value,
• Iim_x→b f(x) exists ( LHL = RHL at x = b), and
• Iim_x→b f(x) = f(b) i.e., Iim_x→b- f(x) = f(b) = Iim_x→b+ f(x).

4. What is Discontinuity?

A function is said to be discontinuous when the condition of continuity ” the limit should be equal to the value at that point” criteria is not satisfied. If seen practically if we cannot draw the curve with a single stroke then also it is discontinuous.

5. Name Three types of Discontinuity.

There are three different kinds of discontinuities:

• Jump Discontinuity
• Point Discontinuity
• Infinite Discontinuity