There are many resistances in complex electrical circuits. There are methods to calculate the equivalent resistances in case multiple resistances are connected in series or parallel or sometimes in a combination of series and parallel. In many situations, batteries or different types of voltage sources are also present in circuits. It is essential to determine their effect on the circuit, thus it’s important to derive the results for calculating the series and parallel combinations of different voltage sources present in the circuit. Let us look at this concept in detail.
Combination of Cells
Often in real life, it is not feasible to make voltage sources and batteries for every particular voltage value. There are only certain types of batteries available on market. In a case, where a different voltage is necessary. Two or more voltage sources are used in different combinations to produce the desired value of voltage and current. These batteries can be connected in two basic types of combinations. These combinations make up the foundation for all other combinations. These two combinations are:
- Series Combination
- Parallel Combination.
Series Combination
In the figure given below, two cells are given which are connected in series with each other. In this case, one terminal of each cell is connected to the other one, and the other terminal is free in either of the cells. E1 and E2 are the emf’s of two cells and r1, r2 are their internal resistances. If the potential at the three points A, B, and C is denoted by V(A), V(B), and V(C). Then the potential differences across these cells are given by V(A) – V(B) and V(B) – V(C).

VAB = V(A) – V(B) = E1 – Ir1
VBC = V(B) – V(C) = E2 – Ir2
Thus, the potential difference between the points A and C will be given by,
V(A) – V(C) = [V(A) – V(B)] – [V(C) – V(B)]
⇒ V(A) – V(C) = E1 + E2 – (Ir1 + Ir2)
⇒ V(A) – V(C) = E1 + E2 – (Ir1 + Ir2)
To replace this combination of cells with a single equivalent cell of emf value Eeq and req. Then,
⇒ Eeq – I(req) = E1 + E2 – (Ir1 + Ir2)
Eeq = E1 + E2 and req = r1 + r2
This can be extended to any number of cells, Eeq = E1 + E2 + … and req = r1 + r2 + …
In this case, connected the negative electrode of the battery are connected to the positive electrode of another battery. In case we connect their similar electrodes together, the two emf’s will now point in opposite directions. In that case, the equivalent values will be,
E = E1 – E2 + … and req = r1 + r2 + …
Parallel Combination
The figure below describes a parallel combination of batteries, in this combination cells are connected in parallel. E1 and E2 are the emf’s of two cells and r1, r2 are their internal resistances. This time, the current flowing through each cell is different and they are denoted by I1 and I2 while the total current flowing through the circuit is denoted by I and is the sum of both of the two currents.
I = I1 + I2

Let V(B1) and V(B2) denote the potential at B1 and B2. Consider both the cells one by one,
V = V(B1) – V(B2) = E1 – I1R
V = V(B1) – V(B2) = E2 – I2R
I = I1 + I2
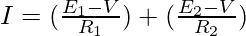
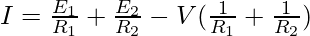
Rearranging the equation to take out the value of V,
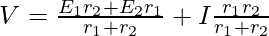
To replace this combination of cells with a single equivalent cell of emf value Eeq and req. Then,
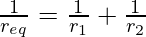
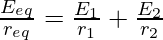
Sample Problems
Question 1: Batteries of 10V and 5 V are connected in series such that their emf’s point in the same direction. Find the equivalent resistance for the system.
Answer:
The formula for equivalent series emf is given by,
Eeq = E1 + E2 + …
Given: E1 = 10, E2 = 5
Substituting these values in the equation,
E = E1 + E2
⇒ E = 10 + 5
⇒ E = 15 V
Question 2: Batteries of 3, 5, and 10 ohms are connected in series such that their emf’s point in the same direction. Find the equivalent resistance for the system.
Answer:
The formula for equivalent series emf is given by,
Eeq = E1 + E2 + …
Given: E1 = 3, E2 = 5and E3 = 10
Substituting these values in the equation,
E = E1 + E2 + E3
⇒ E = 3 + 5 + 10
⇒ E = 18 V
Question 3: Batteries of 10V and 5 V are connected in series such that their emf’s point in the same direction. The internal resistances of the batteries are 2 and 10 ohms respectively. Find the equivalent resistance for the system.
Answer:
The formula for equivalent series emf is given by,
Eeq = E1 + E2 + …
Given: E1 = 10, E2 = 5
Substituting these values in the equation,
E = E1 + E2
⇒ E = 10 + 5
⇒ E = 15 V
Equivalent resistance is also given by a similar equation,
req = r1 + r2 +
Given: r1 = 2, r2 = 10
substituting these values in the equation,
r = r1 + r2
⇒ r = 2 + 10
⇒ r = 12 ohms
Question 4: Three batteries of internal resistances 2, 2, and 4 ohms are connected in parallel. Find the equivalent resistance for the system.
Answer:
The formula for equivalent resistance is given by,
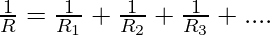
Given: R1 = 2, R2 = 2 and R3 = 4
Substituting these values in the equation,
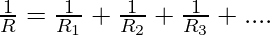
⇒ 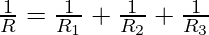
⇒ 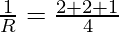
⇒ 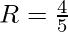
Question 5: Three batteries of internal resistances 5, 5 ohm, and 10, 10 V are connected in parallel. Find the equivalent resistance and emf for the system.
Answer:
The formula for equivalent resistance is given by,
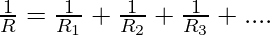
Given: R1 = 5, R2 = 5
Substituting these values in the equation,
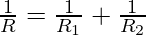
⇒ 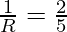
⇒ 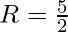
The equivalent emf is given by,
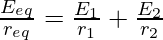
⇒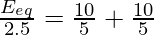
⇒ 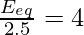
⇒ Eeq = 10 V
Share your thoughts in the comments
Please Login to comment...