Chi-square distance in Python
Last Updated :
19 Jul, 2021
Chi-square distance calculation is a statistical method, generally measures similarity between 2 feature matrices. Such distance is generally used in many applications like similar image retrieval, image texture, feature extractions etc. The Chi-square distance of 2 arrays ‘x’ and ‘y’ with ‘n’ dimension is mathematically calculated using below formula :
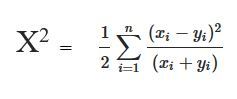
In this article, we will learn how to calculate Chi-square distance using Python. Below given 2 different methods for calculating Chi-square Distance. Let’s see both of them with examples.
Method #1: Calculating Chi – square distance manually using above formula.
Python3
import numpy as np
def chi2_distance(A, B):
chi = 0.5 * np.sum([((a - b) ** 2) / (a + b)
for (a, b) in zip(A, B)])
return chi
if __name__== "__main__":
a = [1, 2, 13, 5, 45, 23]
b = [67, 90, 18, 79, 24, 98]
result = chi2_distance(a, b)
print("The Chi-square distance is :", result)
|
Input : a = [1, 2, 13, 5, 45, 23]
b = [67, 90, 18, 79, 24, 98]
Output : The Chi-square distance is : 133.55428601494035
Input : a = [91, 900, 78, 30, 602, 813]
b = [57, 49, 36, 759, 234, 928]
Output : The Chi-square distance is : 814.776999405035
Method #2: Using scipy.stats.chisquare() method
Syntax: scipy.stats.chisquare(f_obs, f_exp=None, ddof=0, axis=0)
Parameters:
==> f_obs : array1
==> f_exp : array2, optional
==> ddof(Delta degrees of freedom – adjustment for p-value) : int, optional
==> axis : int or None, optional
The default value of ddof and axis is 0.
Returns:
==> chisq : float or ndarray
==> p-value of the test : float or ndarray
Python3
from scipy.stats import chisquare
k = [3, 4, 6, 2, 9, 5, 2]
print(chisquare(k))
|
Output :
Power_divergenceResult(statistic=8.516129032258064, pvalue=0.20267440425509237)
Share your thoughts in the comments
Please Login to comment...