Check whether two numbers are in silver ratio
Last Updated :
11 Jul, 2022
Given two numbers A and B, the task is to check that A and B are in silver ratio.
Silver Ratio: Two numbers are said to be in silver ratio if the ratio of the sum of the smaller and twice the larger number to the larger number is the same as the ratio of the larger one to the smaller one. Below is the representation of the silver ratio:
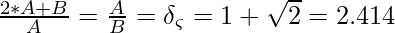
for A > 0, B > 0
Examples:
Input: A = 2.414, B = 1
Output: Yes
Explanation:
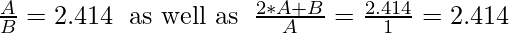
Input: A = 1, B = 0.414
Output No
Explanation: Ratio of A to B do not form a golden ratio
Approach: The idea is to find two ratios and check whether they are equal to the silver ratio(2.414).
// Here A denotes the larger number
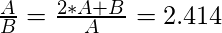
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
bool checksilverRatio(float a, float b)
{
if(a < b)
swap(a, b);
float ratio1 = ((a / b) * 1000.0) / 1000.0;
float ratio2 = (int)(((2 * a + b) /
a) * 1000);
ratio2 = ratio2 / 1000;
if (ratio1 == ratio2 &&
(int)(ratio1 - 2.414) == 0)
{
cout << "Yes\n";
return true;
}
else
{
cout << "No\n";
return false;
}
}
int main()
{
float a = 2.414;
float b = 1;
checksilverRatio(a, b);
}
|
Java
import java.util.*;
import java.lang.*;
class GFG{
static boolean checksilverRatio(double a,
double b)
{
if (a < b)
{
a = a + b;
b = a - b;
a = a - b;
}
double ratio1 = ((a / b) * 1000) / 1000;
double ratio2 = (int)(((2 * a + b) /
a) * 1000);
ratio2 = ratio2 / 1000;
if (ratio1 == ratio2 &&
(int)(ratio1 - 2.414) == 0)
{
System.out.println("Yes");
return true;
}
else
{
System.out.println("No");
return false;
}
}
public static void main(String[] args)
{
double a = 2.414;
double b = 1;
checksilverRatio(a, b);
}
}
|
Python3
def checksilverRatio(a, b):
a, b = max(a, b), min(a, b)
ratio1 = round(a / b, 3)
ratio2 = round((2 * a + b)/a, 3)
if ratio1 == ratio2 and\
ratio1 == 2.414:
print("Yes")
return True
else:
print("No")
return False
if __name__ == "__main__":
a = 2.414
b = 1
checksilverRatio(a, b)
|
C#
using System;
class GFG{
static bool checksilverRatio(double a,
double b)
{
if (a < b)
{
a = a + b;
b = a - b;
a = a - b;
}
double ratio1 = ((a / b) * 1000) / 1000;
double ratio2 = (int)(((2 * a + b) /
a) * 1000);
ratio2 = ratio2 / 1000;
if (ratio1 == ratio2 &&
(int)(ratio1 - 2.414) == 0)
{
Console.WriteLine("Yes");
return true;
}
else
{
Console.WriteLine("No");
return false;
}
}
public static void Main()
{
double a = 2.414;
double b = 1;
checksilverRatio(a, b);
}
}
|
Javascript
<script>
function checksilverRatio(a, b)
{
if (a < b)
{
a = a + b;
b = a - b;
a = a - b;
}
let ratio1 = ((a / b) * 1000) / 1000;
let ratio2 = Math.floor(((2 * a + b) /
a) * 1000);
ratio2 = ratio2 / 1000;
if (ratio1 == ratio2 &&
(ratio1 - 2.414) == 0)
{
document.write("Yes");
return true;
}
else
{
document.write("No");
return false;
}
}
let a = 2.414;
let b = 1;
checksilverRatio(a, b);
</script>
|
References: https://en.wikipedia.org/wiki/Silver_ratio
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...