Check if Pascal’s Triangle is possible with a complete layer by using numbers upto N

Given a number N, the task is to determine if it is possible to make Pascal’s triangle with a complete layer by using total number N integer if possible print Yes otherwise print No.

Note: Pascal’s triangle is a triangular array of the binomial coefficients. Following are the first 6 rows of Pascal’s Triangle. 

1  
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1 
1 5 10 10 5 1 

In Pascal’s Triangle from the topmost layer there is 1 integer, at every next layer from top to bottom size of the layer increased by 1.

Examples:

Input: N = 10
Output: Yes
Explanation:
You can use 1, 2, 3 and 4 integers to make first, second, third, and fourth layer of pascal’s triangle respectively and also N = 10 satisfy by using (1 + 2 + 3 + 4) integers on each layer = 10.
Input: N = 5 
Output: No
Explanation:
You can use 1 and 2 integers to make first and second layer respectively and after that you have only 2 integers left and you can’t make 3rd layer complete as that layer required 3 integers.

Approach: Here we are using integer 1, 2, 3, … on every layer starting from first layer, so we can only make Pascal’s triangle complete if it’s possible to represent N by the sum of 1 + 2 +…

1. The sum of first X integers is given by 
   

1. We can only make pascal’s triangle by using N integers if and only if 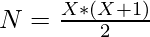where X must be a positive integer. So we have to check is there any positive integer value of x exist or not.
2. To determine value of X from second step we can deduced the formula as: 
   

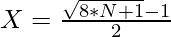
1. If the value of X integer for the given value of N then we can make Pascal Triangle. Otherwise, we can’t make Pascal Triangle.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to check if Pascaltriangle
// can be made by N integers
void checkPascaltriangle(int N)
{
    // Find X
    double x = (sqrt(8 * N + 1) - 1) / 2;

    // If x is integer
    if (ceil(x) - x == 0)
        cout << "Yes";

    else
        cout << "No";
}

// Driver Code
int main()
{
    // Given number N
    int N = 10;

    // Function Call
    checkPascaltriangle(N);
    return 0;
}

Java

// Java program for the above approach
class GFG{

// Function to check if Pascaltriangle
// can be made by N integers
static void checkPascaltriangle(int N)
{

    // Find X
    double x = (Math.sqrt(8 * N + 1) - 1) / 2;

    // If x is integer
    if (Math.ceil(x) - x == 0)
        System.out.print("Yes");
    else
        System.out.print("No");
}

// Driver Code
public static void main(String[] args)
{

    // Given number N
    int N = 10;

    // Function call
    checkPascaltriangle(N);
}
}

// This code is contributed by amal kumar choubey

Python3

# Python3 program for the above approach
import math

# Function to check if Pascaltriangle
# can be made by N integers
def checkPascaltriangle(N):

    # Find X
    x = (math.sqrt(8 * N + 1) - 1) / 2

    # If x is integer
    if (math.ceil(x) - x == 0):
        print("Yes")
    else:
        print("No")

# Driver Code

# Given number N
N = 10

# Function call
checkPascaltriangle(N)

# This code is contributed by sanjoy_62

C#

// C# program for the above approach
using System;

class GFG{

// Function to check if Pascaltriangle
// can be made by N integers
static void checkPascaltriangle(int N)
{

    // Find X
    double x = (Math.Sqrt(8 * N + 1) - 1) / 2;

    // If x is integer
    if (Math.Ceiling(x) - x == 0)
        Console.Write("Yes");
    else
        Console.Write("No");
}

// Driver Code
public static void Main(String[] args)
{

    // Given number N
    int N = 10;

    // Function call
    checkPascaltriangle(N);
}
}

// This code is contributed by amal kumar choubey

Javascript

<script>

      // JavaScript program for the above approach

      // Function to check if Pascaltriangle
      // can be made by N integers
      function checkPascaltriangle(N) {
        // Find X
        var x = (Math.sqrt(8 * N + 1) - 1) / 2;

        // If x is integer
        if (Math.ceil(x) - x == 0)
        document.write("Yes");
        else
        document.write("No");
      }

      // Driver Code

      // Given number N
      var N = 10;

      // Function Call
      checkPascaltriangle(N);

    </script>

Output:

Yes

Time Complexity: O(sqrt(N)) 
Auxiliary Space: O(1)