Check if difference of areas of two squares is prime
Last Updated :
14 Aug, 2022
Given two squares with side lengths 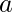 and
and 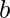 (a > b). The task is to check if difference of their areas is prime or not. Here side length could be large ( 1 < b < a < 1012).
(a > b). The task is to check if difference of their areas is prime or not. Here side length could be large ( 1 < b < a < 1012).
Examples:
Input : a = 6, b = 5
Output : Yes
Input : a = 61690850361, b = 24777622630
Output : No
Approach: Since the sides are 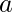 and
and 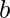 . Therefore, difference of their areas = (a2 – b2), which can be expressed as (a – b)(a + b) . This is prime if and only if a – b = 1 and a + b is a prime . Since a+b is at most 2×1012, we can use trial division to check its primality.
. Therefore, difference of their areas = (a2 – b2), which can be expressed as (a – b)(a + b) . This is prime if and only if a – b = 1 and a + b is a prime . Since a+b is at most 2×1012, we can use trial division to check its primality.
Below is the implementation of the above idea:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPrime(long long int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (long long int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
bool isDiffPrime(long long int a, long long int b)
{
if (isPrime(a + b) && a - b == 1)
return true;
else
return false;
}
int main()
{
long long int a = 6, b = 5;
if (isDiffPrime(a, b))
cout << "Yes";
else
cout << "No";
return 0;
}
|
Java
class GFG
{
static boolean isPrime(long n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (long i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
static boolean isDiffPrime(long a, long b)
{
if (isPrime(a + b) && a - b == 1)
return true;
else
return false;
}
public static void main(String []args)
{
long a = 6, b = 5;
if (isDiffPrime(a, b))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
C#
using System;
class GFG
{
static bool isPrime(long n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (long i = 5;
i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
static bool isDiffPrime(long a, long b)
{
if (isPrime(a + b) && a - b == 1)
return true;
else
return false;
}
public static void Main()
{
long a = 6, b = 5;
if (isDiffPrime(a, b))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Python3
def isPrime(n) :
if (n <= 1) :
return False
if (n <= 3) :
return True
if (n % 2 == 0 or n % 3 == 0) :
return False
i = 5
while(i * i <= n) :
if (n % i == 0 or n % (i + 2) == 0) :
return False
i = i + 6
return True
def isDiffPrime(a, b):
if (isPrime(a + b) and a - b == 1):
return True
else:
return False
a = 6
b = 5
if (isDiffPrime(a, b)):
print("Yes")
else:
print("No")
|
PHP
<?php
function isPrime($n)
{
if ($n <= 1)
return false;
if ($n <= 3)
return true;
if ($n % 2 == 0 || $n % 3 == 0)
return false;
for($i = 5; $i * $i <= $n;
$i = $i + 6)
if ($n % $i == 0 ||
$n % ($i + 2) == 0)
return false;
return true;
}
function isDiffPrime($a, $b)
{
# when a+b is prime and a-b is 1
if (isPrime($a + $b) &&
$a - $b == 1)
return true;
else
return false;
}
$a = 6;
$b = 5;
if (isDiffPrime($a, $b))
echo "Yes";
else
echo "No";
?>
|
Javascript
<script>
function isPrime(n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for(let i = 5; i * i <= n;
i = i + 6)
if (n % i == 0 ||
n % (i + 2) == 0)
return false;
return true;
}
function isDiffPrime(a, b)
{
if (isPrime(a + b) &&
a - b == 1)
return true;
else
return false;
}
let a = 6;
let b = 5;
if (isDiffPrime(a, b))
document.write("Yes");
else
document.write("No");
</script>
|
Time Complexity: O(sqrtn)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...